Ejercicios propuestos de sistemas dinámicos, estimación y control
Ejercicios propuestos del libro Sistemas Dinámicos en Contexto. Se invita al lector a resolver los problemas y comprobar la solución con MATLAB u otra herramienta computacional. Ver también los ejercicios resueltos y los problemas propuestos más elaborados en forma de prácticas con MATLAB (pequeño proyecto de laboratorio en computador).
1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 1.10, 1.11, 1.12, 1.13, 1.14, 1.15, 1.16, 1.17, 1.18, 1.19, 1.20, 1.21, 1.22, 1.23, 1.24
2. Modelación matemática y simulación de sistemas dinámicos
2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7
3. Análisis de sistemas dinámicos
3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8
4. Diseño de sistemas básicos de control lineal
5. Identificación de sistemas dinámicos
5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8, 5.9, 5.10
1. Fundamentos matemáticos
1.1. Ecuaciones diferenciales de primer orden
Dadas las siguientes ecuaciones diferenciales y sus condiciones iniciales, (i) especificar las características de la ecuación (tipo, orden, variable dependiente, variable independiente, término independiente); (ii) hallar la solución general por el método adecuado, indicando el intervalo de definición de la solución; (iii) aplicar el teorema de existencia y unicidad al problema de valor inicial; (iv) resolver el problema de valor inicial; (v) reemplazar la solución en la ecuación diferencial para verificar el resultado; (vi) bosquejar la forma de la solución, es decir, graficar aproximadamente la solución de un problema sin necesidad de utilizar las proporciones correctas, lo cual implica una comprensión adecuada de dicha solución; (vii) utilizar las herramienta de matemáticas simbólicas de MATLAB para verificar los resultados y graficar la solución particular, tal y como se muestra en el código de MATLAB que se puede acceder desde este sitio web.
- $\dot{y}+2y=0, y(0) =1$
- $\dot{P}=kP, P(0) =1$. La ecuación modela el crecimiento de la población de una especie cuando hay recursos ilimitados, donde $P$ es el tamaño de la población, $t$ se da en días y $k=0.5$ es la constante de proporcionalidad que depende del medio y de la tasa reproductiva de la especie. En ese caso es natural que la velocidad de crecimiento $\dot{P}$ en un tiempo determinado sea proporcional a la población $P\left( t \right) $ en ese instante. ¿Cuál es el valor de $k$ si se tiene una población de bacterias y $P(10) =10$?
- $\dot{y}=\frac{t}{y},y(0) =0$
- $\dot{y}=\frac{t}{y},y(0) =1$
- $\dot{y}=\frac{y}{t},y(0) =0$
- $\dot{y}=\frac{y}{t},y(1) =0$
- $\dot{y}=\frac{y}{t},y(1) =1$
- $\dot{y}=y(1+\frac{1}{t}) ,y(0) =1$
- $\dot{y}=y(1+\frac{1}{t}) ,y(1) =0$
- $\dot{y}=y(1+\frac{1}{t}) ,y(1) =1$
- $\dot{y}=4\sqrt{y}\cos 2t,y(0) =0$
- $\dot{h}=-\frac{A_o\sqrt{2gh}}{A_t},h(0) =1$. La ecuación modela la salida de líquido de un tanque por un orificio, donde $h$ es la altura del tanque en metros, $g=9.8~\mathrm{m/{s}^2}$ es la aceleración de la gravedad, $A_o=\pi (0.05)^2~\mathrm{m}^2$ es el área del orificio y $A_t=\pi(1)^2~\mathrm{m}^2$ es el área de la base del tanque. ¿En cuánto tiempo se vacía el 80 % del tanque?
- $\dot{T}=k(T-T_m) ,T(0) =200$. La ecuación modela el proceso de enfriamiento de un cuerpo en contacto con el ambiente, donde $k=-0.2~\mathrm{s^{-1}}$ es la constante de proporcionalidad que depende de la forma de contacto del cuerpo con el medio (tamaño y material), $T$ es la temperatura del cuerpo en grados Celsius y $T_m=20~{\mathrm{°C}}$ es la temperatura del medio que lo rodea. ¿A cuánto es igual $k$ si un cuerpo alcanza la temperatura de $\mathrm{100~°C}$ en 30 minutos?
- $\dot{P}=P(a-bP) ,P(0) =1,a=1,b=2$. El modelo corresponde a la ecuación logística de población $P(t)$, la cual tiene en cuenta una capacidad máxima.
- $\dot{P}=P(a-bP) ,P(0) =1,a=2,b=1$
- $\dot{y}+2y=u_s(t-1) ,y(0) =1$
- $T\dot{y}+y=1,T=0.5,y(0) =0$
- $T\dot{y}+y=\left\{ \begin{matrix}0,& t<1\\ 1,& t\geqslant 1\\ \end{matrix} \right. $ . Donde, $T=1.5,y(0)=2$
- $\dot{y}+5y=e^{-t},y(0) =1$
- $\dot{y}+5y=1+e^{-5t},y(0) =1$
- $\dot{y}-y=2t,y(0) =2$
- $\dot{y}+2y=3e^{-2t},y(0) =2$
- $\dot{y}+3y=\sin t, y(0) =0$
- $m\dot{v}=mg-fv,v(0) =0$. La ecuación modela la caída libre de un cuerpo en la Tierra desde cierta altura y en cierto medio viscoso, donde $g=9.8~\mathrm{m/{s}^2}$ es la aceleración de la gravedad, $m=1~\mathrm{kg}$ es la masa del cuerpo y $f=0.01~\mathrm{kg/s}$ es la fuerza de fricción del medio. ¿La velocidad aumenta indefinidamente o se estabiliza en algún valor?
- $\dot{V}=\lambda e^{-\alpha t}V, V(0) =2$. La ecuación modela el crecimiento de un tumor, donde $\alpha =0.3$ y $\lambda =1$ son constantes positivas, $V(t) $ es el volumen del tumor en $mm^3$ y $t$ está dado en meses.
- $Ldi/dt+Ri=V_e(t) ,i(0) =0$. La ecuación modela un circuito eléctrico básico RL en serie, donde $i(t)$ es la corriente en amperios, $V_e(t) =10\sin0.1t$ es el voltaje aplicado en voltios (V), $R=10~\Omega$ es la resistencia eléctrica en ohmios y $L=0.1~\mathrm{H}$ es la inductancia en henrios.
- $Ldi/dt+Ri=V_e(t) ,i(0) =0$. Donde, los parámetros (constantes) son las mismas del ejercicio anterior y $V_e(t) =10~\mathrm{V}$.
- $\dot{y}=-2y+e^{-3t},y(0) =2$
- $\dot{y}=4y+e^{-t},y(0) =-1$
- $t^2\dot{y}=y-ty, y(-1) =-1$
- $(t+1) \dot{y}+y=\ln t,y(1) =10$
- $(t+1) \dot{y}=3+y,y(0) =-4$
- $t\dot{y}+(3t+1)y=e^{-3t},y(1) =0$
- $\dot{y}\cos t+y\sin t=0,y(0) =2$
- $\dot{y}+3t^2y-t^2=0,y(0) =1/3$
- $\dot{y}+y\ln t=0,y(1) =e^{-1}$
- $t^2\dot{y}+t(t+2) y=e^t,y(1) =e/2$
- $\dot{y}=-2y+e^{-2t},y(0) =1$
- $\dot{y}=\frac{ty}{t+1},y(1)=1/2$
- $t\dot{y}+y=te^t, y(1) =0$
- $\dot{y}=\frac{y-4}{t-3},y(0) =3$
- $t\dot{y}+2y=3,y(1) =2$
1.2. Ecuaciones diferenciales de orden superior
Dadas las siguientes ecuaciones diferenciales y sus condiciones iniciales, (i) especificar las características de la ecuación (tipo, orden, variable dependiente, variable independiente, término independiente); (ii) hallar la solución genera por el método de las raíces características para la solución de la ecuación homogénea y el método de coeficientes indeterminados para la solución de la ecuación no homogénea; (iii) reemplazar la solución en la ecuación diferencial para verificar el resultado; (iv) resolver el problema de valor inicial para hallar la solución particular de toda la ecuación diferencial; (v) bosquejar la forma de la solución; (vi) utilizar las herramienta de matemáticas simbólicas de MATLAB para verificar los resultados y graficar la solución particular, tal y como se muestra en el código de MATLAB que se puede acceder desde este sitio web; (vii) dada la solución, obtener la ecuación diferencial homogénea.
- $\ddot{y}+2\dot{y}+3y=0,y(0)=1,\dot{y}(0)=2$
- $\ddot{y}+3\dot{y}+2y=1,y(0)=\dot{y}(0)=0$
- $\ddot{y}+2\dot{y}+y=1,y(0)=\dot{y}(0)=0$
- $\ddot{y}=2, y(0) =1,\dot{y}(0) =0$
- $\dddot{y}=1,y(0)=\dot{y}(0)=\ddot{y}(0)=0$
- $\overset{(4)}{y}+2\ddot{y}+y=1,y(0)=\dot{y}(0)=\ddot{y}(0)=\dddot{y}(0)=0$
- $\overset{(4)}{y}+2\ddot{y}+y=0,y(0)=\dot{y}(0)=\ddot{y}(0)=\dddot{y}(0)=0$. Resolverla mentalmente sin un procedimiento matemático y explicar.
- $\ddot{y}+y=\sin t,y(0)=\dot{y}(0)=0$
- $\overset{(4)}{y}+2\ddot{y}+y=1,y(0)=\dot{y}(0)=\ddot{y}(0)=\dddot{y}(0)=0$
- $\dddot{y}+1.25\ddot{y}+0.4\dot{y}=1+\cos 2.5t,y(0)=1,\dot{y}(0)=0,\ddot{y}(0)=0$
- $\dddot{y}+4\ddot{y}+3\dot{y}=\dot{u}+u,u=e^{-t},y(0)=\dot{y}(0)=\ddot{y}(0)=0$
- $\ddot{y}+y=f(t),y(0)=0,\dot{y}(0)=1,f(t)=\left\{ \begin{matrix} 0,& 0\leqslant t<\pi\\ 1,& \pi \leqslant t<2\pi\\ 0,& t\geqslant 2\pi\\\end{matrix} \right. $
- $\overset{(5)}{y}+\overset{(4)}{y}=1+t\sin t+\cos t,\mathrm{c.i. = 0}$
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0$. La ecuación modela el movimiento de un sistema masa-resorte en un medio viscoso, donde $y(t)$ es el desplazamiento en metros de la masa con respecto a la posición de equilibrio, $m=1~\mathrm{kg}$ es la masa del cuerpo y $f=0.1~\mathrm{kg/s}$ es la fricción viscosa (depende del medio y la forma del cuerpo), $k=4~\mathrm{N/m }$ es el valor de la constante elástica. Si la fuerza externa es igual a cero ($F_{ext}=0~\mathrm{N}$) se tiene un movimiento libre amortiguado. Indicar el cuasiperíodo y la cuasifrecuencia angular.
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0$. Con $m=1$, $f=0$, $k=4$ y $F_{ext}=0$. Movimiento libre no amortiguado. Indicar la amplitud, el período, la frecuencia angular y el valor medio del desplazamiento alrededor del cual oscila el sistema.
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0$. Con $m=1$, $f=0.1$, $k=4$ y $F_{ext}=1$. Movimiento forzado amortiguado. Indicar el cuasiperíodo, la cuasifrecuencia angular y el valor del desplazamiento en el que se estabiliza.
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0$. Con $m=1$, $f=0$, $k=4$ y $F_{ext}=1$. Movimiento forzado no amortiguado. Indicar la amplitud, el período, la frecuencia angular y el valor medio del desplazamiento alrededor del cual oscila el sistema.
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0$. Con $m=1$, $f=0$, $k=4$ y $F_{ext}=\sin2t$. Movimiento forzado no amortiguado con resonancia. Explicar el fenómeno de resonancia.
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0$. Con $m=1$, $f=0$, $k=4$ y $F_{ext}=\sin t$. Movimiento forzado no amortiguado sin resonancia. Explicar por qué no se da el fenómeno de resonancia.
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0$. Con $m=1$, $f=0.1$, $k=4$ y $F_{ext}=\sin 2t$. Movimiento forzado amortiguado con cuasirresonancia. Explicar el fenómeno de cuasirresonancia. Tomar un valor máximo de tiempo igual a 120 para observar mejor el resultado.
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0$. Con $m=1$, $f=0.1$, $k=4$ y $F_{ext}=\sin t$. Movimiento forzado amortiguado sin cuasirresonancia. Explicar por qué no se da el fenómeno de cuasirresonancia. Tomar un valor máximo de tiempo igual a 120 para observar mejor el resultado.
- $\dddot{y}+3\ddot{y}+2\dot{y}=0, y(0)=0, \dot{y}(0) =2, \ddot{y}(0) =0$
- $\overset{(4)}{y}+9\ddot{y}=0, y(0)=1, \dot{y}(0)=0, \ddot{y}(0) =0, \dddot{y}(0) =0$
- $\overset{(4)}{y}+2\dddot{y}=0, y(0)=0, \dot{y}(0)=-2, \ddot{y}(0) =4, \dddot{y}(0) =-8$
- $\dddot{y}+2\ddot{y}+2\dot{y}=0, y(0)=0, \dot{y}(0) =0,\ddot{y}(0) =-1$
- $\dddot{y}+2\ddot{y}+\dot{y}=0, y(0)=0, \dot{y}(0) =0,\ddot{y}(0) =-1$
- $\dddot{y}+16\dot{y}=0, y(0) =0, \dot{y}(0) =4,\ddot{y}(0) =0$
- $\overset{(4)}{y}+\ddot{y}=0, y(0)=0, \dot{y}(0)=0, \ddot{y}(0) =-1, \dddot{y}(0) =0$
- $\overset{(4)}{y}+\ddot{y}=0, y(0)=1, \dot{y}(0)=1, \ddot{y}(0)=0, \dddot{y}(0) =-1$
- $\ddot{y}+4\dot{y}+13y=0,y(0)=0,\dot{y}(0)=-2$
- $\overset{(4)}{y}+4\dddot{y}+13\ddot{y}=0$
- $\overset{(4)}{y}-6\dddot{y}+13\ddot{y}=0$
- $\ddot{y}+2\dot{y}=1+e^t,y(0)=0,\dot{y}(0)=0$
- $\ddot{y}-\dot{y}=3+e^t,y(0)=0,\dot{y}(0)=0$
1.3. Método de Euler para ecuaciones de primer orden
Dadas las siguientes ecuaciones diferenciales de primer orden, (i) obtener la respectiva ecuación recursiva por método de Euler con el paso $T_s$ (o período de muestreo) que se indica; (ii) hallar manualmente los primeros cinco valores de la solución numérica; (iii) implementar el método en MATLAB y graficar la solución; (iv) comparar el resultado con el obtenido con las funciones dsolve y ode45 de MATLAB; (v) interpretar el resultado. Ver los ejercicios propuestos 2.6 para la aplicación del método de Euler a ecuaciones diferenciales de orden superior.
- $\dot{y}+2y=0,y(0)=1$, $T_s=0.1$
- $\dot{P}=kP,P(0)=1$, $T_s=0.1$, $k=0.2~\mathrm{s}^{-1}$
- $\dot{y}=\frac{t}{y},y(0)=0$, $T_s=0.1$
- $\dot{y}=\frac{t}{y},y(0)=1$, $T_s=0.1$
- $\dot{y}=\frac{y}{t},y(0)=0$, $T_s=0.1$
- $\dot{y}=\frac{y}{t},y(1)=0$, $T_s=0.1$
- $\dot{y}=\frac{y}{t},y(1)=1$, $T_s=0.2$
- $\dot{y}=y(1+\frac{1}{t}) ,y(0)=1$, $T_s=0.1$
- $\dot{y}=y(1+\frac{1}{t}) ,y(1)=0$, $T_s=1$
- $\dot{y}=y(1+\frac{1}{t}) ,y(1)=1$, $T_s=0.2$
- $\dot{y}=4\sqrt{y}\cos 2t,y(0)=0$, $T_s=0.1$
- $\dot{h}=-A_o{{\sqrt{2gh}/A_t}},h(0)=1$, $T_s=0.8$. Donde $g=9.8~\mathrm{m/{s}^2}$, $A_o=\pi (0.05)^2~\mathrm{m^2}$ y $A_t=\pi (1)^2~\mathrm{m^2}$.
- $\dot{T}=k(T-T_m),T(0)=200$, $T_s=0.2$. Donde $k=-0.2~\mathrm{s^{-1}}$ y $T_m=20~\mathrm{°C}$
- $\dot{P}=P(a-bP),P(0)=1,a=1,b=2$, $T_s=0.1$
- $\dot{P}=P(a-bP),P(0)=1,a=2,b=1$, $T_s=0.1$
- $T\dot{y}+y=1,T=0.5,y(0)=0$, $T_s=0.1$
- $\dot{y}+5y=e^{-t},y(0)=1$ , $T_s=0.1$
- $\dot{y}+5y=1+e^{-5t},y(0)=1$, $T_s=0.2$
- $\dot{y}-y=2t,y(0)=2$, $T_s=0.1$
- $\dot{y}+2y=3e^{-2t},y(0)=2$, $T_s=0.5$
- $\dot{y}+3y=\sin t,y(0)=0$, $T_s=0.1$
- $m\dot{v}=mg-fv,v(0)=0$. Donde $g=9.8~\mathrm{m/{s}^2}$, $m=1~\mathrm{kg}$ y $f=0.01~\mathrm{kg/s}$
- $\dot{V}=\lambda e^{-\alpha t}V,V(0)=2$, $T_s=0.5$. Donde $\alpha =0.3$ y $\lambda =1$
- $Ldi/dt+Ri=V_e(t), i(0)=0$, $T_s=0.1$. Donde, $V_e(t) =10\mathrm{sen}0.1t$, $R=10~\mathrm{\Omega}$ y $L=0.1~\mathrm{H}$
- $Ldi/dt+Ri=V_e(t),i(0)=0$, $T_s=0.5$. Donde los parámetros son las mismos del ejercicio anterior
- $\mathbf{\dot{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\\end{matrix} \right] \mathbf{x},\mathbf{x}\left( 0 \right) =\left[ \begin{array}{c} 1\\ 1\\\end{array} \right] ,T_s=0.1$
- $\mathbf{\dot{x}}=\left[ \begin{matrix} 2& 3\\ 2&1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] u,u=1,\mathbf{x}(0) =\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] , T_s=0.1$
- $\mathbf{\dot{x}} = \left[ \begin{matrix} 0 & 1\\ -1& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0 \\ 1\\\end{array} \right] u, u=1, \mathbf{x}(0)=\left[ \begin{array}{c} 1 \\ 0\\\end{array} \right], T_s=0.1$
- $\dot{y}=4\sqrt{y}\cos 2t,y(1)=1$, $T_s=0.1$
- (*) $\dot{y}+2y=u_s(t-1),y(0)=1$ . Entrada definida por partes
- (*) $T\dot{y}+y=\left\{ \begin{matrix} 0,& t<1\\ 1,& t\geqslant 1\\\end{matrix} \right., T=1.5,y(0)=2$. Entrada definida por partes
1.4. Ecuaciones en diferencias lineales
Dadas las siguientes ecuaciones en diferencias y sus condiciones iniciales (si las condiciones iniciales no son adecuadas, seleccionar otras para que el problema tenga solución), (i) especificar las características de la ecuación (tipo, orden, variable dependiente, variable independiente, término independiente); (ii) resolver analíticamente el problema de valor inicial por el método de las raíces características y el método de coeficientes indeterminados; (iii) obtener iterativamente los cinco primeros términos de la solución y compararlos con la solución analítica obtenida previamente; (iv) bosquejar la solución antes de graficar con MATLAB; (v) graficar y comparar la solución analítica e iterativa con MATLAB; (vi) interpretar los resultados.
- $y(k+1)-0.6y(k)=0,y(0)=1$
- $y(k+2)-4y(k+1)+3y(k)=0,y(0)=0,y(1)=1$
- $y(k+2)+0.1y(k+1)-0.02y(k)=0,y(0)=0,y(1)=-1$
- $y(k+2)-0.25y(k)=0,y(0)=1,y(1)=0$
- $y(k+2)-0.25y(k)=0,y(0)=0,y(1)=-1$
- $y(k)-0.25y(k-2)=0,y(0)=0,y(1)=-1$
- $y(k+3)+0.8y(k+2)=0,y(0)=1,y(1)=0,y(2)=1$
- $y(k+2)+0.4y(k+1)+0.04y(k)=0,y(0)=1,y(1)=0$
- $y(k+5)-0.2y(k+4)-0.35y(k+3) =0, y(0)=1,y(1)=0,y(2)=-1,y(3)=0,y(4)=1$
- $y(k+2)-y(k+1)+y(k)=0,y(0)=1,y(1)=-1$
- $y(k+2)-y(k+1)+0.41y(k)=0,y(0)=0,y(1)=-1$
- $y(k+1)-0.6y(k)=2,y(0)=0$
- $y(k+1)-0.6y(k)=0.6^k,y(0)=-0.5$
- $y(k+1)-0.6y(k)=u_s(k-1),y(0)=1$
- $y(k+1)-0.6y(k)=u_s(k-2),y(0)=1$
- $y(k+1)-0.3y(k)=2,y(0)=0.5$
- $y(k+1)-0.3y(k)=k+3,y(0)=2$
- $y(k+1)-0.3y(k)=0.3^k,y(0)=0.3$
- $y(k+1)-0.3y(k)=\sin k,y(0)=0.3$
- $y(k+1)-0.3y(k)=u_s(k-2)-u_s(k-4),y(0)=2$
- $y(k+2)-0.4y(k+1)+0.04y(k)=1,y(0)=0,y(1)=0$
- $y(k+2)-0.4y(k+1)+0.04y(k)=u_s(k-1),y(0)=0,y(1)=0$
- $y(k+2)-0.4y(k+1)+0.04y(k)=k+1,y(0)=0,y(1)=0$
- $y(k+2)-0.4y(k+1)+0.04y(k)=0.2^k,y(0)=0,y(1)=-1$
- $y(k+2)-0.4y(k+1)+0.04y(k)=\sin 0.2k,y(0)=0,y(1)=-1$
- $y(k+2)-0.4y(k+1)+0.04y(k)=u_s(k-1),y(0)=y(1)=0$
- $y(k)-y(k-1)=0,y(0)=0.1$
- $y(k)-y(k-1)=u(k),u(k)=1,y(0)=0.1$
- $y(k)-y(k-1)=u(k),u(k)=-1,y(0)=0$
- $y(k)+y(k-1)=u(k),u(k)=(-1)^k,y(0)=1$
- $y(k)+y(k-1)=u_s(k-1)-u_s(k-2),y(0)=1$
- $y(k+1)+ay(k)=u(k+1)+au(k),u(k)=k,y(0)=0$
- $\left\{ \begin{array}{l} x(k+1) =y(k)\\y(k+1)=1-0.4x(k)\\\end{array} \right., x(0)=-1,y(0)=1$
- $y(k+2)+4y(k) =8\times 2^ku_s(k) ,y(0) =0,y(1) =0$
- $y(k+2)+4y(k) =8\times 2^k\sin (\pi k/2) u_s(k) ,y(0) =0,y(1) =0$
- $y(k+2)+4y(k) =2^{k-1}u_s(k-1) ,y(0) =y(1) =0$
1.5. Efecto del período de muestreo
1.6. Transformada de Laplace
Dadas las siguientes funciones temporales, (i) calcular la transformada de Laplace aplicando las transformadas básicas y las propiedades (los ejercicios de más abajo pueden utilizar las propiedades anteriores a esa); (ii) verificar la solución con la función laplace de MATLAB. Nota: si el ejercicio se puede resolver de diferentes maneras (aplicando una propiedad u otra, o simplemente aplicando una transformada básica), se recomienda hacerlo con cada una de ellas.
A. Transformadas básicas y linealidad- $y(t)=1-t+\sin t$
- $y(t)=4-3t^4+\cos 3t$
- $y(t)=\cos 4t-4\sin 3t$
- $y(t)=1.23e^{0.8t}+4.3e^{-3t}+\frac{1}{5}e^{-6.5t}$
- $y(t)=\frac{1-4t^2}{5}$
- $y(t)=(t+3)^2$
- $y(t)=(t^2+4t+2)^2$
- $y(t)=(t+5)^4$
- $y(t)=\sin (2t+4)$
- $y(t)=\cos(t-6)$
- $y(t)=2\sin 3t\cos 3t$
- $y(t)=te^t$
- $y(t)=te^{-t}$
- $y(t)=t^3e^{-5t}$
- $y(t)=e^{8t}e^{-5t}$
- $y(t)=4e^t$
- $y(t)=e^{-6t}\sin 8t$
- $y(t)=e^{2.4t}\sin 6.5t$
- $y(t)=e^{-\frac{t}{3}}\sin (t/2)$
- $y(t)=e^{-6t}\sin (-8t)$
- $y(t)=e^{-4t}\cos 3t$
- $y(t)=e^{-8t}\cos (-3t)$
- $y(t)=e^{-t}\cos (-6t/5) $
- $y(t)=t^{12}e^{21t}$
- $y(t)=t^4e^{-3.5t}$
- $y(t)=t^4e^{-\frac{t}{5}}$
- $y(t)=e^{-4t}\cos 3(t+2)$
Adicionalmente, representar la función $y(t)$ en las tres formas: por partes, gráficamente y con la función escalón unitario.
- $y(t)=(t-2) u_s(t-2)$
- $y(t)=u_s(t-2)$
- $y(t)=(t-2)^2u_s(t-2)$
- $y(t)=e^{2(t-1)}u_s(t-1)$
- $y(t)=tu_s(t-2)$
- $y(t)=t^2u_s(t-2)$
- $y(t)=(t-3)^2u_s(t-2)$
- $y(t)=e^{2t}u_s(t-1)$
- $y(t)=(t-1)e^{2t}u_s(t-1)$
- $y(t)=\left\{ \begin{matrix} 0,& 0\leqslant t<2\\ 1,& 2\leqslant t<4\\ 0,& t\geqslant 4\\\end{matrix} \right. $
- $y(t)=\left\{ \begin{matrix} -1,& 0\leqslant t<1\\ t-2,& 1\leqslant t<3\\ 3,& t\geqslant 3\\\end{matrix} \right. $
- $y(t)=\left\{ \begin{matrix} t,& 0\leqslant t<2\\ 4-t,& 2\leqslant t<4\\ 0,& t\geqslant 4\\\end{matrix} \right. $
- $y(t)=tu_s(t-2)+u_s(t-4)$
- $y(t)=(t-1)\left[ u_s(t-2)+u_s(t-4) \right] $
- Función dada por el siguiente código de MATLAB:
- sym t; y = t^2 - (t^2 - 1)*heaviside(t-2) - heaviside(t-6); fplot(y), ylim([0 5]), xlim([0 10]), grid, xlabel('t'), ylabel('y(t)')
- Función gráfica:
- Función gráfica
- $y(t)=1*t=\int\limits_0^t{(t-\tau )d\tau}=t*1=\int\limits_0^t{\tau d\tau}$
- $y(t)=t*e^{-t}=\int\limits_0^t{\tau e^{t-\tau}d\tau}=e^{-t}*t=\int\limits_0^t{e^{-\tau}(t-\tau )d\tau}$
- $y(t)=\int\limits_0^t{\tau d\tau}=t*1$
- $y(t)=\int\limits_0^t{(t-\tau )d\tau}$
- $y(t)=\int\limits_0^t{\tau (t-\tau )d\tau}$
- $y(t)=\int\limits_0^t{\tau \cos\mathrm{(}t-\tau )d\tau}$
- $y(t)=\int\limits_0^t{\cos ^2(\tau )d\tau}$
- $y(t)=\int\limits_0^t{e^{\tau}\cos\mathrm{(}t-\tau )d\tau}$
- $y(t)=te^t$
- $y(t)=t$
- $y(t)=t^2$
- $y(t)=t\sin 4t$
- $y(t)=t^2\sin 4t$
- $y(t)=e^{-3t}t^2\sin 4t$
- $y(t)=e^{-3t}t^2\sin 4tu_s(t-1)$
- $y(t)=3\delta (t-4)$
- $y(t)=\delta (t-4)+2\delta (t-6)$
- $y(t)=(t-4)\delta (t-4)$
- $y(t)=e^t\delta (t)$
- $y(t)=e^{t-6}\delta (t)$
- $y(t)=e^t\delta (t)$
- $y(t)=\sin (t-2)\delta (t-1)$
- $y(t)=e^{-6t}\cos t\sin (t-2)\delta (t-1)$
- $y(t)=e^{t-2}u_s(t-2)\delta (t-1)$
- $y(t)=e^{t-2}u_s(t-2)\delta (t-5)$
- $y(t)=e^t*\delta (t)$
Aplicar los teoremas del valor inicial y el valor final a los ejercicios anteriores. Es decir, calcular el valor inicial y el valor final a partir de la función temporal y a partir de su transformada de Laplace, y verificar que coinciden.
1.7. Transformada inversa de Laplace
Dadas las siguientes transformadas de Laplace, (i) calcular la función temporal continua $y(t)$ (transformada inversa de Laplace) a partir de la tabla de transformadas básicas y propiedades (los ejercicios de más abajo pueden utilizar las propiedades anteriores a esa); (ii) comprobar la solución con la función ilaplace de MATLAB. Nota: si el ejercicio se puede resolver de diferentes maneras (aplicando una propiedad u otra, o simplemente aplicando una transformada básica), se recomienda hacerlo por cada una de ellas.
A. Transformadas básicas y linealidad- $Y(s)=\frac{4}{s}$
- $Y(s)=\frac{3}{s^2}$
- $Y(s)=\frac{1}{s^3}$
- $Y(s)=\frac{s+1}{s^5}$
- $Y(s)=\frac{s^3+7s+1}{s^5}$
- $Y(s)=\frac{4}{s+1}$
- $Y(s)=\frac{4}{s-1}$
- $Y(s)=\frac{4}{s+1}-\frac{4}{s^2+1}$
- $Y(s)=\frac{1}{s^2+2}-\frac{s}{s^2+2}$
- $Y(s)=\frac{1}{s^2+\frac{1}{4}}-\frac{s}{s^2+\frac{1}{9}}$
- $Y(s)=\frac{1}{2}\left( \frac{3.5}{s}-\frac{1}{s+1.4}-\frac{4.8}{s^2+7.2}+\frac{2.3s}{s^2+3.8} \right) $
- $Y(s)=\frac{1}{s-1}$
- $Y(s)=\frac{1}{(s-1)^2}$
- $Y(s)=\frac{s}{s^2+4s+7}=\frac{s}{(s+2)^2+3}$
- $Y(s)=\frac{3}{s^2-2s+1}$
- $Y(s)=\frac{1}{(s+1)^2}$
- $Y(s)=\frac{s-2}{s^2+2s+1}$
- $Y(s)=\frac{s-2}{s^2-4s+4}$
- $Y(s)=\frac{1}{(s+1)^6}$
- $Y(s)=\frac{3}{(s+1)^2+4}$
- $Y(s)=\frac{3}{(s-8)^2+4}$
- $Y(s)=\frac{s+1}{(s+1)^2+4}$
- $Y(s)=\frac{s-7}{(s-7)^2+4}$
- $Y(s)=\frac{s+5}{(s+1)^2+4}$
- $Y(s)=\frac{s+1}{s^2+2s+5}$
- $Y(s)=\frac{s-7}{s^2-14s+53}$
- $Y(s)=\frac{s+1}{(s-7)^2+4}$
- $Y(s)=\frac{s}{(s-7)^2+4}-\frac{1}{(s+2)^2+9}$
- $Y(s)=\frac{1}{4}\left[ \frac{1}{(s+0.2)^3}-\frac{5s}{(s+0.5)^2+4}-\frac{3}{(s+2.5)^2+8} \right] $
- $Y(s)=\frac{s+1}{s^2-2s+2}$
- $Y(s)=\frac{s-1}{s^2-2s+3.8}$
- $Y(s)=\frac{s+3}{s^2+6s+13}$
- $Y(s)=\frac{1}{(s+1)(s+2)}$
- $Y(s)=\frac{s}{(s+1)(s+2)}$
- $Y(s)=\frac{s^2}{(s+1)(s+2)}$
- $Y(s)=\frac{1}{(s+1)(s+2)(s+3)}$
- $Y(s)=\frac{1}{(s+1)(s+2)(s+3)(s+4)}$
- $Y(s)=\frac{s^2}{(s+1)(s+2)(s+3)(s+4)}$
- $Y(s)=\frac{1}{(s+1)(s+2)^2}$
- $Y(s)=\frac{1}{(s+1)^2(s+2)^2}$
- $Y(s)=\frac{1}{(s+3)(s+4)}+\frac{1}{s(s+5)^2}$
- $Y(s)=\frac{1}{(s+3)(s+4)}+\frac{1}{(s+5)^2}$
- $Y(s)=\frac{1}{s^2+4s+5}+\frac{1}{(s+5)^8}$
- $Y(s)=\frac{1}{(s+1)(s^2+4)}$
- $Y(s)=\frac{1}{(s+1)^2(s^2+4)}$
- $Y(s)=\frac{1}{s(s+1)(s+2)^2}$
- $Y(s)=\frac{1}{s(s+1)(s+2)^2(s^2+3)}$
- $Y(s)=\frac{1}{(s+1)\left[ (s+1)^2+4 \right]}$
- $Y(s)=\frac{1}{(s-3)\left[ (s-3)^2+4 \right]}$
- $Y(s)=\frac{1}{(s-4)\left[ (s-3)^2+4 \right]}$
- $Y(s)=\frac{s-3}{(s-4)\left[ (s-3)^2+4 \right]}$
- $Y(s)=\frac{1}{(s+1)(s^2+2s+5)}$
- $Y(s)=\frac{1}{(s^2+2s+4)(s^2+2s+5)}$
En este ejercicio, indicar la función $y(t)$ en tres formas: por partes, con la función escalón unitario y gráficamente.
- $Y(s)=\frac{e^{-2s}}{s}$
- $Y(s)=\frac{3e^{-4s}}{s}$
- $Y(s)=\frac{e^{-2s}}{s^2}$
- $Y(s)=\frac{e^{-2s}}{s^4}$
- $Y(s)=\frac{e^{-3s}}{s+3}$
- $Y(s)=\frac{e^{-3s}}{s^2+9}$
- $Y(s)=\frac{se^{-3s}}{s^2+9}$
- $Y(s)=\frac{e^{-6s}}{s^2+5}$
- $Y(s)=\frac{e^{-6s}}{s+5}$
- $Y(s)=\frac{e^{-6s}}{s+5}$
- $Y(s)=\frac{1}{s}-\frac{e^{-2s}}{s}+\frac{3e^{-4s}}{s^2}+\frac{2e^{-7s}}{s+1}$
- $Y(s)=\frac{e^{-6s}}{(s+5)^2}$
- $Y(s)=\frac{e^{-2s}}{(s-3)^3}$
- $Y(s)=\frac{(s+1)e^{-3s}}{(s+1)^2+9}$
- $Y(s)=\frac{(s-2)e^{-3s}}{(s+3)^2+16}$
- $Y(s)=\frac{e^{-6s}-3e^{-7s}+2e^{-4s}}{(s+5)^2}$
- $Y(s)=\frac{1}{s(s+1)}$
- $Y(s)=\frac{1}{s^2}$
- $Y(s)=\frac{1}{s^2(s+1)}$
- $Y(s)=\frac{1}{(s+1)(s+2)}$
- $Y(s)=\frac{1}{s(s^2+1)}$
- $Y(s)=\frac{1}{s^2(s^2+1)}$
- $Y(s)=\frac{s}{s+1}$
- $Y(s)=\frac{s+3}{s+1}$
- $Y(s)=\frac{s^2}{s^2+1}$
- $Y(s)=\frac{(s+1)^2}{(s+1)^2+4}$
- $Y(s)=\frac{s^2+4s+5}{s^2+4s+6}$
- (*) $Y(s)=\frac{s^2}{s+1}$
- (*) $Y(s)=\frac{s^3}{(s+1)(s+2)}$
- $Y(s)=\frac{e^{-4s}}{(s+1)(s+2)(s+3)}$
- $Y(s)=\frac{e^{-3s}}{(s+1)(s+2)}$
- $Y(s)=\frac{e^{-3s}}{(s+1)\left[ (s+1)^2+4 \right]}$
- $Y(s)=\frac{(s+1)e^{-3s}}{(s^2+2s+4)(s^2+2s+5)}$
Aplicar los teoremas del valor inicial y el valor final a los ejercicios anteriores. Es decir, calcular el valor inicial y el valor final a partir de la función temporal y a partir de su transformada de Laplace, y verificar que coinciden.
1.8. Aplicación de la transformada de Laplace
Dadas las siguientes ecuaciones diferenciales, aplicar las fórmulas básicas y las propiedades de la transformada de Laplace para: (i) calcular $Y(s)$; (ii) calcular la transformada inversa de $Y(s)$ dejando indicados los coeficientes de las fracciones parciales cuando aplique (solución $y(t)$ de la ecuación diferencial); (iii) calcular los coeficientes de las fracciones parciales cuando aplique y dar la solución final de la ecuación diferencial; (iv) bosquejar el gráfico de la solución; (v) verificar la solución con las funciones simbólicas de MATLAB (ilaplace, laplace, partfrac, dsolve).
A. Solución de ecuaciones diferenciales lineales simplesEn estos ejercicios se aplican las propiedades de linealidad y traslación compleja de la transformada de Laplace.
- $\dot{y}=0,y(0)=1$
- $\dot{y}=1,y(0)=0$
- $\dot{y}+2y=0,y(0)=1$
- $\dot{y}+2y=1,y(0)=0$
- $\dot{y}+2y=e^{-3t},y(0)=0$
- $\dot{y}+2y=\mathrm{sen}3t,y(0)=0$
- $\dot{y}+2y=1+4e^{-2t}-5\sin 3t,y(0)=0$
- $\dot{y}=\cos t,y(0)=0$
- $\dot{y}+2y=\cos 2t,y(0)=0$
- $\ddot{y}=0,y(0)=1,\dot{y}(0)=0$
- $\ddot{y}=1+2t+t^2,y(0)=0,\dot{y}(0)=0$
- $\ddot{y}=1,y(0)=0,\dot{y}(0)=0$
- $\ddot{y}+4y=0,y(0)=1,\dot{y}(0)=0$
- $\ddot{y}+4y=0,y(0)=0,\dot{y}(0)=1$
- $\ddot{y}+4y=0,y(0)=0,\dot{y}(0)=1$
- $\ddot{y}+2\dot{y}+y=0,y(0)=-1,\dot{y}(0)=1$
- $\ddot{y}+2\dot{y}+y=1,y(0)=0,\dot{y}(0)=0$
- $\ddot{y}+2\dot{y}+y=t^2e^{-t},y(0)=0,\dot{y}(0)=0$
- $\ddot{y}+3\dot{y}+2y=0,y(0)=1,\dot{y}(0)=0$
- $\ddot{y}+3\dot{y}+2y=1,y(0)=\dot{y}(0)=0$
- $\dddot{y}+3\ddot{y}+2\dot{y}=1,y(0)=\dot{y}(0)=\ddot{y}(0)=0$
- $\dddot{y}+3\ddot{y}+2\dot{y}=e^{-2t},y(0)=\dot{y}(0)=\ddot{y}(0)=0$
- $\ddot{y}+2\dot{y}+5y=0,y(0)=1,\dot{y}(0)=0$
- $\ddot{y}+2\dot{y}+5y=0,y(0)=0,\dot{y}(0)=1$
- $\ddot{y}+4y=\mathrm{sen}t,y(0)=\dot{y}(0)=0$
- $\ddot{y}+4\dot{y}=te^{-3t},y(0)=\dot{y}(0)=0$
- $\dddot{y}=0,y(0)=1,\dot{y}(0)=2,\ddot{y}(0)=-1$
- $\dddot{y}=1,y(0)=\dot{y}(0)=\ddot{y}(0)=0$
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0,m=1,k=2,f=1,F_{ext}=1$
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0,m=1,k=2,f=2,F_{ext}=1$
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0,m=1,k=1,f=0,F_{ext}=1$
En estos ejercicios se aplican todas las fórmulas básicas y las propiedades de la transformada de Laplace para hallar la solución. Además, verificar la solución por simulación (función lsim de MATLAB) .
- $\dddot{y}+1.25\ddot{y}+0.4\dot{y}=1+\cos 2.5t,y(0)=1,\dot{y}(0)=0,\ddot{y}(0)=0$
- $\overset{(5)}{y}+\overset{(4)}{y}=1+t\sin t+\cos t,\mathrm{c.i. = 0}$
- $\ddot{y}+4y=u_s(t-1)) -2u_s(t-2), y(0) =\dot{y}(0)) =2$
- $\ddot{y}+y=f(t), y(0)=0,\dot{y}(0)=1,f(t)=\left\{ \begin{matrix} 0,& 0\leqslant t<\pi\\ 1,& \pi \leqslant t<2\pi\\ 0,& t\geqslant 2\pi\\\end{matrix} \right. $
- $\dot{y}+y=f(t) ,y(0) =1,f(t) =\left\{ \begin{array}{l} e^{-t}, & 0\le t<3\\0, & t \ge 3\\ \end{array} \right. $
- $\dot{y}+y=f(t), y(0) =0,f(t)=\left\{ \begin{matrix}t, &0 \le t<1\\ 0, &t\ge 1\\ \end{matrix} \right. $
- $\ddot{y}+y=f(t), y(0)=0,\dot{y}(0)=1,f(t)=\left\{ \begin{matrix} 0,& 0\leqslant t<\pi\\ 1,& \pi \leqslant t<2\pi\\ 0,& t\geqslant 2\pi\\\end{matrix} \right. $
- $\dot{y}+3y=g(t), y(0) =1$
- $\dot{y}+y=f(t), y(0) =3$
- (*) $\ddot{y}+2ty=0,y(0)=0,\dot{y}(0)=0$
En estos ejercicios se aplican todas las fórmulas básicas y las propiedades de la transformada de Laplace para hallar la solución. Además, verificar la solución por simulación (función lsim de MATLAB) .
- $\left\{\begin{array}{l} \dot{x}=-y\\ \dot{y}=x\\ \end{array}\right. ~~x(0)=2,y(0)=0$
- $\left\{ \begin{array}{l} \dot{x}=-x-3y\\ \dot{y}=x-y \\\end{array} \right. ~~x(0)=1,y(0)=0$
- $\left\{ \begin{array}{l} \dot{x}=2x-y+1\\ \dot{y}=x+2y \\\end{array} \right. ~~x(0)=1,y(0)=-1$
- $\int\limits_0^t{y(x)dx}=t$
- $\int\limits_0^t{y(x)dx}=e^{-t}$
- $\int\limits_0^t{y(x)dx}=\cos t$
- $\int\limits_0^t{y(x)dx}=y(t)$
- $\int\limits_0^t{y(x)dx}=te^{-t}$
- $\int\limits_0^t{y(x)dx}=t\cos t$
- $\dot{y}+\int\limits_0^t{y(x)dx}=1,y(0)=0$
- $y(t)-2\int\limits_0^t{\sin (t-\tau)y(\tau )d\tau}=\sin t$
1.9. Transformada z de funciones de tiempo discreto
Dadas las siguientes funciones de tiempo discreto, (i) calcular la transformada z (función $Y(z)$) aplicando las transformadas básicas y las propiedades; (ii) verificar la solución con la función ztrans de MATLAB; (iii) aplicar los teoremas del valor inicial y el valor final.
- $y(k)=1+k+2^{-k}$
- $y(k)=3^ku_s(k)$
- $y(k)=3^k$
- $y(k)=e^{-3k}+e^{-k}$
- $y(k)=(\frac{1}{2})^k-2(-\frac{2}{5})^k$
- $y(k)=2\sin 3k$
- $y(k)=\delta (k)-0.7\delta (k-3)$
- $y(k)=\sin (k-2)u_s(k-2)$
- $y(k)=k-4$
- $y(k)=(k-4)u_s(k-4)$ (en muchas ocasiones se debe multiplicar por la función escalón unitario adecuada para evitar confusiones)
- $y(k)=\left[ \left( \frac{1}{2} \right)^{k-1} - 2\left( -\frac{2}{5} \right) ^{k-1} \right] u_s(k-1)$
- $y(k)=\left\{ \begin{array}{l}3^k,& 0 \le k<2\\ 0,& k\ge 2\\ \end{array} \right.$
- $y(k)=\delta (k)-\delta (k-1)$
- $y(k)=2^kk$
- $y(k)=(k-1)2^{k-1}u_s(k-1)$
- $y(k)=\sum_{i=0}^k{i5^{k-i}}$
- $y(k)=\sum_{i=0}^k{0.5^i}$
- $y(k)=(-4)^k\sin k$
- $y(k)=(-4)^{k-5}\sin (k-5)u_s(k-5)$
1.10. Transformada z inversa
Dadas las siguientes transformadas z, (i) calcular la función temporal discreta $y(k)$ (transformada inversa z) a partir de la tabla de transformadas básicas y propiedades; (ii) calcular y comparar los 5 primeros valores a partir de la función temporal, la división larga y la respectiva ecuación en diferencias; (iii) aplicar los teoremas del valor inicial y el valor final; (iv) verificar la solución con la función iztrans de MATLAB.
- $Y\left( z \right) =\frac{z}{z+0.5}$
- $Y\left( z \right) =\frac{1}{z+0.5}$
- $Y\left( z \right) =\frac{1}{z^2(z+0.5)}$ (aplicar fracciones parciales y el teorema de traslación real)
- $Y\left( z \right) =\frac{1}{z^{20}(z+0.5)}$
- $Y\left( z \right) =\frac{1}{z^2}$
- $Y\left( z \right) =\frac{z}{(z+0.5)(z-0.8)}$
- $Y\left( z \right) =\frac{1}{( z+0.5)(z-0.8)}$
- $Y\left( z \right) =\frac{z^2}{z^2+1}$
- $Y\left( z \right) =\frac{z}{z^2+1}$
- $Y\left( z \right) =\frac{z(z+1)}{z^2+2z+1}$ (ajustar a un seno y también cancelar el polo y el cero)
- $Y\left( z \right) =\frac{z}{z^2+z+1}$
- $Y\left( z \right) =\frac{1}{z^2+z+2}$
- $Y\left( z \right) =\frac{z^2}{z^2+z+2}$
- $Y\left( z \right) =\frac{z}{(z-1)( z^2+z+1)}$
- $Y\left( z \right) =\frac{2}{1-\frac{1}{3}z^{-1}}$
- $Y\left( z \right) =\frac{1-z^{-1}}{1-\frac{1}{4}z^{-2}}$
- $Y\left( z \right) =4z^{-1}-3z^{-2}+5z^{-3}$
- $Y\left( z \right) =\frac{z}{(z-0.5) ^2}$ (usar el teorema de traslación compleja)
1.11. Aplicación de la transformada z
Dadas las siguientes ecuaciones en diferencias, (i) aplicar las fórmulas básicas y las propiedades de la transformada z para hallar la solución; (ii) bosquejar el gráfico de la solución; (iii) verificar la solución analítica comparándola con la solución iterativa en los primeros 5 instantes de muestreo.
- $y(k+1)-0.6y(k)=0,y(0)=1$
- $y(k+2)-4y(k+1)+3y(k)=0,y(0)=0,y(1)=1$
- $y(k+2)+0.1y(k+1)-0.02y(k)=0,y(0)=0,y(1)=-1$
- $y(k+2)-0.25y(k)=0,y(0)=1,y(1)=0$
- $y(k+2)-0.25y(k)=0,y(0)=0,y(1)=-1$
- $y(k)-0.25y(k-2)=0,y(0)=0,y(1)=-1$
- $y(k+3)+0.8y(k+2)=0,y(0)=1,y(1)=0,y(2)=1$
- $y(k+2)+0.4y(k+1)+0.04y(k)=0,y(0)=1,y(1)=0$
- $y(k+5) -0.2y(k+4) -0.35(k+3) =0,y(0)=1,y(1)=0,y(2)=-1,y(3)=0,y(4)=1$
- $y(k+2)-y(k+1)+y(k)=0,y(0)=1,y(1)=-1$
- $y(k+2)-y(k+1)+0.41y(k)=0,y(0)=0,y(1)=-1$
- $y(k+1)-0.6y(k)=2,y(0)=0$
- $y(k+1)-0.6y(k)=0.6^k,y(0)=-0.5$
- $y(k+1)-0.6y(k)=u_s(k-1),y(0)=1$
- $y(k+1)-0.6y(k)=u_s(k-2),y(0)=1$
- $y(k+1)-0.3y(k)=2,y(0)=0.5$
- $y(k+1)-0.3y(k)=k+3,y(0)=2$
- $y(k+1)-0.3y(k)=0.3^k,y(0)=0.3$
- $y(k+1)-0.3y(k)=\sin k,y(0)=0.3$
- $y(k+1)-0.3y(k)=u_s(k-2)-u_s(k-4),y(0)=2$
- $y(k+2)-0.4y(k+1)+0.04y(k)=1,y(0)=0,y(1)=0$
- $y(k+2)-0.4y(k+1)+0.04y(k)=u_s(k-1),y(0)=0,y(1)=0$
- $y(k+2)-0.4y(k+1)+0.04y(k)=k+1,y(0)=0,y(1)=0$
- $y(k+2)-0.4y(k+1)+0.04y(k)=0.2^k,y(0)=0,y(1)=-1$
- $y(k+2)-0.4y(k+1)+0.04y(k)=\sin 0.2k,y(0)=0,y(1)=-1$
- $y(k+2)-0.4y(k+1)+0.04y(k)=u_s(k-1),y(0)=y(1)=0$
- $y(k)-y(k-1)=0,y(0)=0.1$
- $y(k)-y(k-1)=u(k),u(k)=1,y(0)=0.1$
- $y(k)-y(k-1)=u(k),u(k)=-1,y(0)=0$
- $y(k)+y(k-1)=u(k),u(k)=(-1)^k,y(0)=1$
- $y(k)+y(k-1)=u_s(k-1)-u_s(k-2),y(0)=1$
- $y(k+1)+ay(k)=u(k+1)+au(k),u(k)=k,y(0)=0$
- $\left\{ \begin{array}{l} x(k+1) =y(k) \\ y(k+1) =1-0.4x(k)\\\end{array} \right., ~~x(0)=-1,y(0)=1$
- $y(k+2)+4y(k) =8\times 2^k u_s(k) ,y(0) =0,y(1) =0$
- $y(k+2)+4y(k)=8\times 2^k\sin (\pi k/2) u_s(k) ,y(0) =0,y(1) =0$
- $y(k+2)+4y(k) =2^{k-1} u_s(k-1) ,y(0) =y(1) =0$
1.12. Relación entre las variables s y z
Analizar la relación entre las variables s (de la transformada de Laplace) y la variable z (de la transformada z).
1. A partir de $z=e^{T_ss},s=\alpha +i\beta, z = a + ib, T_s=0.1$, diseñar un programa de MATLAB para dibujar las siguientes funciones en el plano s y su equivalente discreto en el plano z:
$\alpha =0,\alpha =1,\alpha =-1,\beta =0,\beta =1,\beta =-1,\beta =\alpha ,\beta =-\alpha $
2. Repetir el ejercicio anterior y analizar el resultado si se utiliza la siguiente aproximación:
$z=e^{Ts}=\frac{e^{\frac{T}{2}s}}{e^{\frac{T}{2}s}}=\frac{1+\frac{T}{2}s+\frac{1}{2}\left( \frac{T}{2}s \right) ^2+\cdots}{1-\frac{T}{2}s+\frac{1}{2}\left( \frac{T}{2}s \right) ^2+\cdots}\approx \frac{1+\frac{T}{2}s}{1-\frac{T}{2}s}$
3. Repetir el ejercicio anterior y analizar el resultado si se utiliza la siguiente aproximación:
$z=e^{Ts}=\frac{e^{\frac{T}{2}s}}{e^{\frac{T}{2}s}}=\frac{1+\frac{T}{2}s+\frac{1}{2}\left( \frac{T}{2}s \right) ^2+\cdots}{1-\frac{T}{2}s+\frac{1}{2}\left( \frac{T}{2}s \right) ^2+\cdots}\approx \frac{1+\frac{T}{2}s+\frac{1}{2}\left( \frac{T}{2}s \right) ^2}{1-\frac{T}{2}s+\frac{1}{2}\left( \frac{T}{2}s \right) ^2}$
4. Repetir el ejercicio anterior y analizar el resultado si se utiliza la siguiente aproximación (bilineal):
$z=\frac{1+s}{1-s}$
1.13. Función de transferencia
A partir de las siguientes ecuaciones diferenciales o en diferencias, (i) obtener la función de transferencia, donde $u(t)$ o $u(k)$ corresponde a la entrada; (ii) determinar los polos y ceros manualmente y verificarlos con las funciones pole y zero de MATLAB; (iii) indicar a partir de los polos y ceros si el sistema es estable y de fase mínima; (iv) especificar si el modelo tiene o no retardo puro.
A. Caso de tiempo continuo- $\ddot{y}+3\dot{y}+2y=u(t) $
- $\ddot{y}+2\dot{y}+y=u(t) $
- $\dddot{y}=u(t) $
- $\overset{(4)}{y}+2\ddot{y}+y=u(t) $
- $\ddot{y}+y=u(t) $
- $\dddot{y}+1.25\ddot{y}+0.4\dot{y}=u(t) $
- $\dddot{y}+4\ddot{y}+3\dot{y}=\dot{u}+u$
- $\overset{(5)}{y}+\overset{(4)}{y}=u(t) $
- $\overset{(5)}{y}+\overset{(4)}{y}=\ddot{u}+\dot{u}$
- $\ddot{y}+3\dot{y}+2y=\dot{u}+2u$
- $\ddot{y}+3\dot{y}+2y=u(t-2) $
- $\dot{y}=u(t)$
- $\dot{y}+y=u(t-3)$
- $y(k+1) -0.6y(k) =u(k) $
- $y(k+2) -4y(k+1) +3y(k) =u(k)$
- $y(k+2) +0.1y(k+1) -0.02y(k) =u(k) $
- $y(k+2) -0.25y(k) =u(k) $
- $y(k+3) +0.8y(k+2) =u(k) $
- $y(k) -y(k-1) =u(k) $
- $y(k+1) -0.6y(k) =u(k+1) +0.2u(k) $
- $y(k+2) -2y(k+1) -3y(k) =u(k+1) -3u(k) $
- $y(k+3) +0.8y(k+2) =u(k+1) +0.8u(k) $
- $y(k+1) +ay(k) =u(k+1) +au(k) $
- $y(k) -y(k-1) =u(k-3) $
- $y(k) -0.25y(k-1) =u(k-4) $
1.14. Respuesta temporal a partir de la función de transferencia
Dadas las siguientes funciones de transferencia, (i) calcular la respuesta temporal con la entrada que se indica; (ii) explicar el comportamiento en términos de la ubicación de los polos y ceros (calcularlos con las funciones pole y zero de MATLAB); (iii) comprobar los teoremas de valor inicial y valor final; (iv) graficar la solución y compararla con los resultados de la función lsim de MATLAB.
A. Caso de tiempo continuo- $G(s)=\frac{1}{s+1},u=1$
- $G(s)=\frac{1}{s+1},u=\sin t$
- $G(s)=\frac{1}{s+1},u=\delta(t)$
- $G(s)=\frac{e^{-2s}}{s+1},u=\delta(t)$
- $G(s)=\frac{1}{s+1},u=\delta(t-2)$
- $G(s)=\frac{s+1}{(s+2)(s+3)},u=1$
- $G(s)=\frac{s-1}{(s+2)(s+3)},u=1$
- $G(s)=\frac{s-1}{(s+2)(s+3)},u=e^t$
- $G(s)=\frac{1}{s^2+s+4},u=1$
- $G(s)=\frac{e^{-3s}}{s^2+s+4},u=1$
- $G(s)=\frac{1}{s^2+s+4},u=\delta (t-3)$
- $G(s)=\frac{s-2}{s^2+s+4},u=1$
- $G(s)=\frac{3(s+1)(s+2)e^{-3s}}{(s+1.2)(s+1.8)(s^2+s+6)},u=1$
- $G(s)=\frac{s+1}{s+2},u=1$
- $G(s)=\frac{s-1}{s-1.001},u=1$
- $G(s)=\frac{s+1}{s+1.001},u=1$
- $\mathbf{G}(s)=\frac{1}{s^2+2s+8}\left[\begin{matrix} s+1& 2\\ \end{matrix} \right], \mathbf{u}=\left[ \begin{matrix} 1\\-1\\ \end{matrix} \right] $
- $\mathbf{G}(s)=\frac{1}{s^2+2s+8}\left[ \begin{array}{c} s+1\\ 2\\\end{array} \right] ,u=1$
- $\mathbf{G}(s)=\frac{1}{(s+1)(s+2)}\left[ \begin{matrix} 1& 0\\ -2& s+3\\ s+4& -(s+4)\\\end{matrix} \right] ,\mathbf{u}=\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] $
- $G(z)=\frac{1}{z+0.1},u=1$
- $G(z)=\frac{1}{z^3(z+0.1)},u=1$
- $G(z)=\frac{z-2}{z(z+0.1)},u=2^k$
- $G(z)=\frac{1}{z^2+0.16},u=1$
- $G(z)=\frac{1}{z^2-0.16},u=1$
- $G(z)=\frac{2(z-0.2)(z+0.3)}{z^2(z-0.22)(z+0.8)(z+0.5)^2},u=\delta (k)$
1.15. Interpretación de la función de transferencia
Dadas las siguientes funciones de transferencia, (i) hallar la respuesta al impulso, es decir, con $u(t)=\delta (t)$; (ii) por la integral de convolución y con la respuesta al impulso anterior, hallar analíticamente la respuesta temporal si la entrada es un escalón unitario; (iii) repetir el ejercicio anterior con una señal sinusoidal; (iv) comparar las respuestas anteriores con la respuesta simulada utilizando la función lsim de MATLAB.
A. Caso continuo- $G(s) =\frac{1}{(s+1)(s+2)}$
- $G(s) =\frac{e^{-2s}}{s+1}$
- $G(s) =\frac{1}{s^2+2s+2}$
- $G(s) =\frac{e^{-3s}}{s^2+2s+2}$
- $G(z) =\frac{0.2z}{z+0.1},T_s=1$
- $G(z) =\frac{0.2z}{z+0.1},T_s=2$
- $G(z) =\frac{3}{z+0.5},T_s=0.2$
- $G(z) =\frac{3}{z-0.5},T_s=0.2$
- $G(z) =\frac{0.6z}{(z-0.1)(z+0.2)},T_s=0.4$
- $G(z) =\frac{3}{z^3(z^2-0.25)},T_s=0.1$
- $G(z) =\frac{0.4}{z^2+0.25},T_s=0.5$
1.16. Discretización de funciones de transferencia
Dadas las siguientes funciones de transferencia de tiempo continuo, (i) seleccionar un período de muestreo adecuado de acuerdo con el tiempo de crecimiento; (ii) discretizar con un retenedor de orden cero y el período de muestreo seleccionado anteriormente; (iii) explicar el comportamiento a partir de los polos y ceros continuos y discretos (en particular, determinar si los polos y ceros de fase no mínima del modelo continuo se conservan al discretizar el modelo); (iv) comprobar los resultados con la función c2d de MATLAB; (v) analizar lo que pasa con los polos y ceros de tiempo discreto si el período de muestreo es demasiado pequeño (0.0001, por ejemplo).
- $G(s)=\frac{1}{s+1}$
- $G(s)=\frac{e^{-2s}}{s+1}$
- $G(s)=\frac{s+1}{(s+2)(s+3)}$
- $G(s)=\frac{s-1}{(s+2)(s+3)}$
- $G(s)=\frac{1}{s^2+s+4}$
- $G(s)=\frac{e^{-3s}}{s^2+s+4}$
- $G(s)=\frac{s-2}{s^2+s+4}$
- $G(s) =\frac{3(s+1)(s+2) e^{-3s}}{(s+1.2) (s+1.8)( s^2+s+6)}$
- $G(s)=\frac{s+1}{s+2}$
- $G(s)=\frac{s-1}{s-1.001}$
- $G(s)=\frac{s+1}{s+1.001}$
- $\mathbf{G}(s)=\frac{1}{s^2+2s+8} \left[ \begin{matrix} s+1& 2\\ \end{matrix} \right], \mathbf{u}=\left[ \begin{array}{c} 1\\-1\\ \end{array} \right]$
1.17. Reducción del orden de funciones de transferencia
Dadas las siguientes funciones de transferencia, (i) reducir el orden por el método de cancelación de polos y ceros, y eliminación de polos insignificantes; (ii) graficar la respuesta a un escalón unitario de la función de transferencia original y la reducida; (iii) analizar los resultados.
- $G(s)=\frac{2(s+4)}{(s+1)(s+3)(s+4.05)}$
- $G(s)=\frac{1.5(s+1.1)(s+4.8)}{(s+1)(s+3)(s+5)}$
- $G(s)=\frac{3.5(s+1.9)}{(s+2)(s^2+2s+2)}$
- $G(s)=\frac{s^2+2s+2}{(s+2)(s^2+2.2s+2.21)}$
- $G(s)=\frac{(s-0.1)(s+0.9)}{(s+1)(s-0.101)(s+2)}$
- $G(s)=\frac{(s-0.1)(s+0.9)}{(s+1)(s-0.1)(s+2)}$
- $G(s)=\frac{3(s+1)(s+2)}{(s+1.9)(s+3)(s+20)}$
- $G(s)=\frac{6.2(s+1.7)}{(s+1.6)(s+18)(s^2+2s+2)}$
- $G(s)=\frac{2.5(s+1.5)(s^2+2s+2)}{(s+1.4)(s+2)(s+10)(s^2+1.8s+1.81)}$
- $G(s)=\frac{1.8(s+2.1)}{(s+2)^2(s^2+2s+2)}$
- $G(s)=\frac{s^2}{(s+0.001)^2(s+2)(s+3)}$ (caso interesante)
- $G(s)=\frac{(s+0.001)^2}{s^2(s+2)(s+3)}$ (caso interesante)
- $G(s)=\frac{1}{(s+0.2)(s+1)(s^2+10s+26)}$ (polos complejos insignificantes)
- $G(s)=\frac{s}{(s+0.2)(s+1)(s^2+10s+26)}$ (caso interesante)
- $G(s)=\frac{s(s+1.1)}{(s+1)(s+2)}$
- $G(s) =\frac{10(s+0.2)}{(s+0.18)^2(s+1)(s+2)(s^2+4s+5)}$
1.18. Ecuación de estado a partir de la ecuación diferencial o en diferencias
Dadas las siguientes ecuaciones diferenciales o en diferencias, (i) obtener la ecuación de estado en variables de fase y, en el caso de modelos lineales, dar la ecuación de estado en forma matricial ($\dot{\mathbf{x}}=\mathbf{Ax}+\mathbf{B}u, y=\mathbf{Cx}$); (ii) especificar el vector de condiciones iniciales (si no se dan las condiciones iniciales, suponer que son iguales a cero).
Nota: en la ecuación de estado no debe quedar ninguna derivada o diferencia de la entrada.
A. Caso de tiempo continuo- $\ddot{y}+2\dot{y}+3y=u(t),y(0)=1,\dot{y}(0)=2$
- $\ddot{y}+2\dot{y}+y=u(t),y(0)=\dot{y}(0)=0$
- $\dddot{y}=u(t),y(0)=\dot{y}(0)=0$
- $\overset{(4)}{y}+2\ddot{y}+y=u(t),y(0)=\dot{y}(0)=\ddot{y}(0)=\dddot{y}(0)=0$
- $\overset{(4)}{y}+2\ddot{y}+y=0,y(0)=\dot{y}(0)=1,\ddot{y}(0)=\dddot{y}(0)=-1$
- $\ddot{y}+y=\sin t,y(0)=0,\dot{y}(0)=1$
- $\overset{(4)}{y}+2\ddot{y}+y=1,y(0)=\dot{y}(0)=1,\ddot{y}(0)=\dddot{y}(0)=0$
- $\dddot{y}+1.25\ddot{y}+0.4\dot{y}=1+\cos t,y(0)=1,\dot{y}(0)=0,\ddot{y}(0)=0$
- $\overset{(5)}{y}+\overset{(4)}{y}=1 + t \sin t + \cos t, \mathrm{c.i. = 0}$
- $m\ddot{y}+f\dot{y}+ky=F_{ext}(t),y(0)=0.5,\dot{y}(0)=0$.
- $\overset{(6)}{y}+3\dddot{y}-2\dot{y}+4y=0,\mathrm{c.i. = 0}$
- $\overset{(5)}{y}+3ty^2\dddot{y}+\sin t \sin y=u(t), \mathrm{c.i. = 1}$
- $\dddot{y}+y=u(t),y(0)=2,\dot{y}(0)=1,\ddot{y}(0)=-1$
- $\overset{(5)}{y}+\overset{(4)}{y}=u(t), \mathrm{c.i. = 1}$
- $\left\{\begin{array}{l} \ddot{x}+3\dot{x}-\dot{y}=u_1\\\dot{y}+2\dot{x}+x-y=u_2\\ \end{array} \right., \mathrm{c.i. = 0}$
- $\left\{ \begin{array}{l} \ddot{r}-r\omega^2+\frac{\mu}{r^2}=0 \\ r\dot{\omega}+2\dot{r}\omega=0\\ \end{array} \right., \mathrm{c.i. = 0}$
- $\ddot{y}+3\dot{y}+4y=u-0.5\dot{u},y(0) =1,\dot{y}(0) =2,u(0) =0$
- $\dddot{y}+3\dot{y}+4y=\ddot{u}-0.5\dot{u},y(0) =1,\dot{y}(0)=\ddot{y}(0)=2, u(0) =0, \dot{u}(0) =0$
- $\dddot{y}+4\ddot{y}+3\dot{y}=\dot{u}+u,y(0)=0, \dot{y}(0)=2, \ddot{y}(0)=-1, u(0) =2$
- $\overset{(5)}{y}+\overset{(4)}{y}=\ddot{u}+\dot{u},\mathrm{c.i. = 0}$
- $\ddot{y}+3\dot{y}+2y=\dot{u}+2u, \mathrm{c.i. = 0}$
- $y(k+5) +k y(k+4) +y^2(k+3) -3\sin k \sin y(k)=u(k) $
- $y(k+3) +0.5y(k) =u(k) +0.5u(k+1)+0.3u(k+2) $
- $y(k+1)-0.6y(k)=u(k)$
- $y(k+2)-4y(k+1)+3y(k)=u(k)$
- $y(k+2)+0.1y(k+1)-0.02y(k)=u(k)$
- $y(k+2) -0.25y(k) =u(k), y(0) =1,y(1) =1$
- $y(k+3) +0.8y(k+2) =u(k), y(0)=1,y(1)=-1,y(2)=2$
- $y(k+1) -0.6y(k) =u(k+1) +0.2u(k), y(0) =2$
- $y(k+2) -2y(k+1) -3y(k) =u(k+1) -3u(k), y(0) =-1, y(1) =-1$
- $y(k+3)+0.8y(k+2)=u(k+1)+0.8u(k)$
- $y(k+1)+ay(k)=u(k+1)+a u(k)$
- $y(k) +3y(k-1) +6y(k-2) =u(k-2), y(0) =-1, y(1)=-2$
- $y(k)-y(k-4)=u(k-1)+0.5u(k-3)$
- $y(k) -y(k-1) =u(k), y(0) =2$
1.19. Solución de la ecuación de estado con valores y vectores propios
Dadas las siguientes ecuaciones de estado o ecuaciones diferenciales (pasar a ecuación de estado con variables de fase) con condiciones iniciales, (i) calcular manualmente los valores y vectores propios; (ii) obtener la matriz de transición del estado y comprobar algunas de sus propiedades (si no se cumplen debe haber un error en la solución hallada); (iii) obtener la solución analítica de la ecuación con la entrada que se indica; (iv) comparar con MATLAB la solución obtenida con la solución simulada utilizando la función lsim; (v) comprobar el cálculo de los valores y vectores propios con la funciones eig o jordan (si hay vectores propios generalizados) de MATLAB.
- $\dot{\mathbf{x}}=\left[\begin{matrix}2&3\\2&1\\ \end{matrix}\right] \mathbf{x},\mathbf{x}(0)=\left[ \begin{array}{c}1\\1\\ \end{array} \right] $
- $\dot{\mathbf{x}}=\left[\begin{matrix} -4& 1& 1\\ 1& 5& -1\\ 0& 1& -3\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\ 1\\ \end{array} \right] $
- $\dot{\mathbf{x}}=\left[\begin{matrix} 1& -2& 2\\ -2& 1& -2\\ 2& -2& 1\\ \end{matrix}\right] \mathbf{x},\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ -1\\ 0\\ \end{array}\right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 3& -18\\ 2& -9\\\end{matrix}\right] \mathbf{x},\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ -1\\ \end{array}\right]$
- $\dot{\mathbf{x}}=\left[\begin{matrix} 2& 1& 6\\ 0& 2& 5\\ 0& 0& 2\\\end{matrix}\right] \mathbf{x},\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ -1\\ 1\\ \end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 8\\ -1& -2\\ \end{matrix}\right] \mathbf{x},\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\ \end{array}\right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\ \end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array} \right]u,u=1,\mathbf{x}(0)=\left[\begin{array}{c} 0\\ 1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\ \end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array}\right]u,u=1,\mathbf{x}(0)=\left[\begin{array}{c} 1\\ -1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\ \end{matrix}\right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array}\right]u,u=\delta (t-2),\mathbf{x}(0)=\left[\begin{array}{c} 1\\ -1\\\end{array}\right] $
- $\dot{\mathbf{x}}=\left[\begin{matrix} 0& 1\\ -1& 0\\ \end{matrix}\right]\mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\\end{array} \right]u,u=1,\mathbf{x}(0)=\left[\begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1\\ -1& 0\\ \end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\ \end{array} \right]u,u=\delta (t),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\ \end{array}\right] $
- $\dddot{y}=u,u=\delta \left( t-1 \right) ,y(0)=1,\dot{y}(0)=0,\ddot{y}(0)=0$
- $\overset{(4)}{y}+5+6\ddot{y}=u,\mathrm{ }u=1,y(0)=\dot{y}(0)=1,\ddot{y}(0)=(0)=0$
- $\dot{\mathbf{x}}=\left[\begin{matrix} -0.0197& 0\\ 0.0178& -0.0129\\ \end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0.0263\\ 0\\ \end{array} \right]u,u=1,\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ -1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1\\ 0& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\ \end{array} \right]u,u=1,\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\ \end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\ \end{array} \right]u(t-2),u=u_s(t),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\ \end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\ \end{array} \right]u(t-0.6),u=u_s(t),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array}\right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\ \end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array} \right]u(t-1.5),u=u_s(t),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[\begin{matrix} 1&0\\ 1&1\\ \end{matrix}\right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 0\\\end{array}\right]u(t-4),u=u_s(t),\mathbf{x}(0)=\left[\begin{array}{c} 0\\ 1\\ \end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 1& 0\\ 1& 1\\ \end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 0\\ \end{array} \right]u(t-0.8),u=u_s(t),\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 1& 0\\ 1& 1\\ \end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 0\\\end{array} \right]u(t-0.8),u=u_s(t),\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] $
1.20. Solución de ecuaciones de estado por transformada de Laplace
1.21. Discretización de la ecuación de estado lineal
1.22. Solución de la ecuación de estado de tiempo discreto
Dadas las siguientes ecuaciones de estado lineales de tiempo discreto, (i) desarrollar un programa en MATLAB para obtener y graficar la solución iterativa si la entrada es un escalón unitario y comparar los resultados con los obtenidos con la función step o lsim de MATLAB, (ii) repetir la tarea anterior si la entrada es una entrada sinusoidal, (iii) resolver analíticamente aplicando la transformada z.
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 1& 0.5\\ 0& 1\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 0.125\\ 0.5\\\end{array} \right] u(k),\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 1& 0.086\\ -0.172& 0.733\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 0.00453\\ 0.0861\\\end{array} \right] u(k),\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.819& 0\\ 0.234& 0.741\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 0.181\\ 0.025\\\end{array} \right] u(k),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} e^{-T}& 0\\ 1-e^{-T}& 1\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 1-e^{-T}\\ T-1+e^{-T}\\\end{array} \right] u(k),T=\{0.1,1\},\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.5& 1\\ 0& -0.2\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] u(k-1),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.5& 1\\ 0& -0.2\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] u(k-2),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} -0.5& 0\\ 0& 0.3\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{matrix} 1& 0\\ 0& 1\\\end{matrix} \right] \mathbf{u}(k),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} -0.5& 0\\ 0& 0.3\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{matrix} 1& 0\\ 0& 1\\\end{matrix} \right] \mathbf{u}(k-3),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} -0.2& 1& 0\\ 0& -0.2& 0\\ 0& 0& 0.5\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 0\\ 1\\ 1\\\end{array} \right] u(k-1),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\ 1\\\end{array} \right] $
1.23. Relación entre la función de transferencia y la ecuación de estado
Dadas las siguientes ecuaciones de estado, (i) obtener analíticamente la función de transferencia o matriz de funciones de transferencia (si no se especifica la salida, suponer que es todo el estado) y verificar los resultados con las funciones ss y tf de MATLAB; (ii) obtener de nuevo la ecuación de estado a partir de la función de transferencia con los comandos anteriores (aunque las ecuaciones de estado tienen diferente forma, son equivalentes); (iii) simular con MATLAB los tres modelos anteriores y mostrar que dan el mismo resultado.
A. Caso de tiempo continuo- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] u,u=1,\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] u,u=1,\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] u,u=\delta (t-2),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1\\ -1& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] u,u=1,\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1\\ -1& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] u,u=\delta (t),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -0.0197& 0\\ 0.0178& -0.0129\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0.0263\\ 0\\\end{array} \right] u,u=1,\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ -1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1\\ 0& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] u,u=1,\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] u(t-2),u=u_s(t),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] u(t-0.6),u=u_s(t),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 3\\ 2& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] u(t-1.5),u=u_s(t),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 1& 0\\ 1& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] u(t-4),u=u_s(t),\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 1& 0\\ 1& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] u(t-0.8),u=u_s(t),\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] $
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 1& 0\\ 1& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] u(t-0.8),u=\sin t,\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 1& 0.5\\ 0& 1\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 0.125\\ 0.5\\\end{array} \right] u(k),\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 1& 0.086\\ -0.172& 0.733\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 0.00453\\ 0.0861\\\end{array} \right] u(k),\mathbf{x}(0)=\left[ \begin{array}{c} 0\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.819& 0\\ 0.234& 0.741\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 0.181\\ 0.025\\\end{array} \right] u(k),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} e^{-T}& 0\\ 1-e^{-T}& 1\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 1-e^{-T}\\ T-1+e^{-T}\\\end{array} \right] u(k),T=\{0.1,1\},\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.5& 1\\ 0& -0.2\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] u(k-1),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.5& 1\\ 0& -0.2\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] u(k-2),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} -0.5& 0\\ 0& 0.3\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{matrix} 1& 0\\ 0& 1\\\end{matrix} \right] \mathbf{u}(k),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} -0.5& 0\\ 0& 0.3\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{matrix} 1& 0\\ 0& 1\\\end{matrix} \right] \mathbf{u}(k-3),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\\end{array} \right] $
- $\mathbf{x}(k+1)=\left[ \begin{matrix} -0.2& 1& 0\\ 0& -0.2& 0\\ 0& 0& 0.5\\\end{matrix} \right] \mathbf{x}(k)+\left[ \begin{array}{c} 0\\ 1\\ 1\\\end{array} \right] u(k-1),\mathbf{x}(0)=\left[ \begin{array}{c} 1\\ 0\\ 1\\\end{array} \right] $
1.24. Transformaciones lineales y formas canónicas diagonal y de Jordan
Dadas las siguientes ecuaciones de estado, (i) transformar a la forma canónica diagonal o forma canónica de Jordan (comprobar los resultados con la función jordan); (ii) resolver la ecuación de estado transformada (más fácil por ser diagonal o cuasidiagonal) por medio de la solución de cada ecuación diferencial, si la entrada es un escalón unitario; (iii) obtener con la función step de MATLAB la respuesta temporal de los modelos original y transformado, y comparar los gráficos con los de la solución de la tarea (ii).
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -4& -3\\ 0& -1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 2\\ -1\\\end{array} \right] u,y=\left[ \begin{matrix} 1& 0\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1\\ -1& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 2\\ -1\\\end{array} \right] u,y=\left[ \begin{matrix} 1& 0\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& -2\\ 1& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 2\\ 1\\\end{array} \right] u,y=\left[ \begin{matrix} 1& 0\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -1& -2\\ 1& -3\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 2\\ 1\\\end{array} \right] u,y=\left[ \begin{matrix} 1& 0\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -1& 0& -1\\ 2& -3& -2\\ 0& 0& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 2\\ 2\\ 1\\\end{array} \right] u,y=\left[ \begin{matrix} 0& 1& 1\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -1& 0& 0\\ 1& -2& -1\\ 0& 0& -1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 2\\ 2\\ 1\\\end{array} \right] u,y=\left[ \begin{matrix} 0& 1& 1\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -6& 0& 4\\ -1& -3& 3\\ -2& 0& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 2\\ 2\\ 1\\\end{array} \right] u,y=\left[ \begin{matrix} 0& 1& 1\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -2& 0& 0& 0\\ -1& -3& -1& 0\\ 0& 0& -2& 0\\ -1& -1& -1& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\ 0\\ 2\\\end{array} \right] u,y=\left[ \begin{matrix} -1& -2& -3& 3\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -2& 0& 1& 0\\ 0& -2& 0& -1\\ -1& -1& -4& 1\\ -2& -2& -3& -1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\ 0\\ 2\\\end{array} \right] u,y=\left[ \begin{matrix} -1& -2& -3& 3\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -3& -1& -1& 1\\ -1& -3& -1& -1\\ 0& 0& -2& 0\\ -2& -2& -2& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\ 0\\ 2\\\end{array} \right] u,y=\left[ \begin{matrix} -1& -2& -3& 3\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -5& 0& 0& 0\\ 1& -4& 2& -1\\ -2& -2& -8& 1\\ -1& -1& -1& -5\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\ 0\\ 2\\\end{array} \right] u,y=\left[ \begin{matrix} -1& -2& -3& 3\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -3& -1& -1& 1\\ 2& 0& 4& -3\\ -3& -3& -7& 2\\ -2& -2& -2& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\ 0\\ 2\\\end{array} \right] u,y=\left[ \begin{matrix} -1& -2& -3& 3\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -3& -2& -2& 2\\ 1& -1& 3& -3\\ -2& -1& -5& 1\\ -2& -1& -1& -3\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\ 0\\ 2\\\end{array} \right] u,y=\left[ \begin{matrix} -1& -2& -3& 3\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -3& -2& -2& 2\\ 5& 3& 9& -5\\ -4& -3& -7& 1\\ 0& 1& 3& -5\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\ 0\\ 2\\\end{array} \right] u,y=\left[ \begin{matrix} -1& -2& -3& 3\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -3& -2& -2& 2\\ 3& 1& 4& -2\\ -1& 0& -2& -1\\ 1& 2& 3& -4\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\ 0\\ 2\\\end{array} \right] u,y=\left[ \begin{matrix} -1& -2& -3& 3\\\end{matrix} \right] \mathbf{x},\mathbf{x}(0)=0$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -4.5& -5.75& -3& 5.75& 3.5& -0.75\\ -2& -1.5& -1& -4.5& -5& -1.5\\ -2.5& 1.25& -7& -2.25& -2.5& 1.25\\ -2& 1& 0& -8& -2& 1\\ 1.5& 6.25& 2& -5.25& -9.5& -1.75\\ 0& 0.5& -1& 0.5& -3& -5.5\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 2\\ 0\\ 2\\ -1\\ 4\\\end{array} \right] u,\mathbf{x}(0)=0,\mathbf{C}=\left[ \begin{array}{c} 0.5\\ 0.75\\ 0\\ 0.25\\ -0.5\\ 0.75\\\end{array} \right] ^T$
2. Modelación matemática y simulación de sistemas dinámicos
2.1. Modelación gráfica de sistemas
- Proceso de aprendizaje profesor-alumno, cuyos objetivos son trazados por el comité del programa y los estudiantes y profesor forman un solo proceso.
- Proceso de aprendizaje profesor-alumno, donde el estudiante controla al profesor para lograr lo que desea
- Proceso de formación de los hijos en una familia, donde los padres ejercen el control
- Proceso de formación de los hijos en una familia, donde los hijos ejercen el control para lograr lo que desean (cosas buenas o malas)
- Proceso de control de tráfico vehicular en una ciudad
- Proceso de control de la contaminación en una ciudad
- Proceso de control de una epidemia en una ciudad
- Proceso de control de la pobreza en una ciudad
- Proceso de control de gastos en una empresa
- Proceso de control de la corrupción en un país
- Proceso de control de la inflación por parte de un organismo estatal
- Sistema de control de nivel de azúcar en el cuerpo por parte del páncreas. Ver páncreas artificial.
- Sistema para mantener una varilla en posición vertical sobre la mano de una persona
- Sistema de control de la temperatura en un salón utilizando aire acondicionado
- Sistema de control de nivel de agua en un tanque de almacenamiento de agua
- Sistema de control de lavado de ropa en una lavadora automática
- Sistema de control adaptativo de crucero (ACC)
2.2. Contextualización de principios sistémicos
2.3. Simplificación de diagramas de bloques
2.4. Simulación con MATLAB
$\left\{ \begin{array}{l} \frac{ds}{dt}=-\alpha si\\ \frac{di}{dt}=\alpha si-\beta i\\\end{array} \right.$
$s(0)=0.8,i(0)=0.2,\beta =0.2,\gamma =0.17 $
2. Circuito RLC en serie$\left\{ \begin{array}{l} L\frac{di}{dt}+Ri+v_c(t)=v_e(t)\\ C\frac{dv_c}{dt}=i(t)\\ \end{array} \right. $
$v_e=10~\mathrm{V},R=20~\mathrm{\Omega}, L=0.2~\mathrm{H}, C=0.0005~\mathrm{F}, i(0)=0~\mathrm{A}, v_c(0)=0~\mathrm{V} $
3. Péndulo simple$\left\{ \begin{array}{l} \dot{x}_1=x_2\\\ \dot{x}_2=-\frac{g}{l}\sin x_1-\frac{f}{m}x_2+\frac{u}{ml}\\ \end{array} \right. $
$x_1=\theta ,x_2=\dot{\theta},\theta(0) =70^{\circ},\dot{\theta}(0) =0~\mathrm{rad/s}, u=F_{ext}=0$
$m=0.45~\mathrm{kg}, l=0.84~\mathrm{m}, g=9.843~\mathrm{m/{s}^2}$
4. Oscilador de resistencia negativa$\left\{ \begin{array}{l} \dot{x}_1=x_2\\ \dot{x}_2=-x_1+\varepsilon (1-x_{1}^{2})x_2\\ \end{array} \right. $
$x_1=v, x_2=\dot{v}, \varepsilon =0.5, x_1(0)= x_2(0)=0 $
5. Modelo presa-depredador$\left\{ \begin{array}{l} \dot{x}_1=\alpha x_1-\beta x_1x_2\\ \dot{x}_2=\delta x_1x_2-\gamma x_2\\ \end{array} \right. $
$x_1=P, x_2=D, \alpha =2, \beta =1.2, \gamma =1, \delta =0.9, P(0)=5, D(0)=3 $
6. Dos tanques acoplados$\left\{ \begin{array}{l} \dot{x}_1=-\frac{k_1}{A_1}\sqrt{x_1-x_2}+\frac{a}{A_1}u\\ \dot{x}_2=\frac{k_1}{A_2}\sqrt{x_1-x_2}-\frac{k_2}{A_2}\sqrt{x_2}\\\end{array} \right. $
$A_1=A_2=0.45~\mathrm{m}^2, a=0.0005~\mathrm{m^3/s}, k_1=0.065~\mathrm{m^{2.5}/s}, k_2=0.047~\mathrm{m^{2.5}/s}, u=[0,100] \% $
7. Sistema de control2.5. Análisis de sensibilidad e incertidumbre
Dados los modelos de los ejercicios propuestos 2.4, realizar las siguientes tareas del análisis de sensibilidad e incertidumbre utilizando la herramienta GSUA de MATLAB. En el caso de los modelos de sistemas de control se debe considerar la incertidumbre en los factores de la planta o proceso.
- Planificar previa y exhaustivamente las pruebas.
- Obtener un gráfico de incertidumbre que muestre los efectos de la propagación de los errores del modelo (parámetros y condiciones iniciales) en relación con la salida nominal. Utilizar un muestreo normal y uno de hipercubo latino con diferente número de muestras y diferentes niveles de incertidumbre de los factores (10%, 20%, 30%, etc.). Analizar el resultado. ¿Hasta qué porcentaje de variación única de los parámetros las predicciones del modelo son confiables?
- Obtener un gráfico de sensibilidad escalar para clasificar los factores de los más a los menos sensibles con diferentes niveles incertidumbre y los métodos OAT, fuerza bruta y Saltelli, en relación con el ajuste a la respuesta temporal nominal en términos de la función del error cuadrático.
- Con base en los resultados del gráfico de sensibilidad, si los índices de sensibilidad son casi nulos, fijarlos en un valor (0 si es posible), repetir los cálculos de incertidumbre y sensibilidad y comparar los resultados. ¿Si tiene sentido fijar esos factores?
- Obtener un gráfico de sensibilidad escalar para clasificar los factores de los más a los menos sensibles con el método de Saltelli en relación con las siguientes características escalares de la respuesta temporal: sobreimpulso máximo, tiempo de pico, tiempo de establecimiento y valor final.
- Interpretar los resultados.
2.6. Método de Euler para ecuaciones de orden superior
- $\ddot{y}+2\dot{y}+3y=0,y(0)=1,\dot{y}(0)=2$
- $\dddot{y}+3\ddot{y}+2\dot{y}=0,y(0) =0, \dot{y}(0) =2, \ddot{y}(0) =0$
- $\ddot{y}+2\dot{y}+y=1,y(0)=\dot{y}(0)=0$
- $\dddot{y}=1,y(0)=\dot{y}(0)=\ddot{y}(0)=0$
- $\ddot{y}+y=\sin t,y\left( 0 \right) =\dot{y}\left( 0 \right) =0$
- $\overset{(4)}{y}+2\ddot{y}+y=1,y(0)=\dot{y}(0)=\ddot{y}(0)=\dddot{y}(0)=0$
- $\overset{(4)}{y}+9\ddot{y}=0, y(0)=1, \dot{y}(0)=0, \ddot{y}(0)=0, \dddot{y}(0) =0$
- $\overset{(4)}{y}+2\dddot{y}=0, y(0)=0, \dot{y}(0)=-2, \ddot{y}(0)=4, \dddot{y}(0)) =-8$
- $\ddot{y}+y=f(t),y(0)=0,\dot{y}(0)=1,f(t)=\left\{ \begin{matrix} 0,& 0\leqslant t<\pi\\ 1,& \pi \leqslant t<2\pi\\ 0,& t\geqslant 2\pi\\\end{matrix} \right. $
- $\ddot{y}+y^2=1,y(0)=0,\dot{y}(0)=1$
- $\ddot{y}+\dot{y}=t,y(0)=-2,\dot{y}(0)=1$
- $\ddot{y}+y=t+1,y(0)=1,\dot{y}(0)=-2$
2.7. Teoría de errores y aproximación
Los siguientes problemas tienen relación con la teoría de errores y aproximación, la cual exige un manejo adecuado de las cifras significativas de las magnitudes medidas y de su propagación a través de operaciones algebraicas.
Expresar los siguientes resultados de manera correcta con el error relativo y el error absoluto con un número de cifras significativas igual a (i) 1, (ii) 2 y (iii) 3.
- $a=1.34256584\pm 0.12345629456$
- $a=2.76852906\pm 1.156789$
- $a=2.34\times 10^{-4}\pm 1.156789\times 10^{-5}$
- $a=34.56\times 10^{-5}\pm 12.27\times 10^{-7}$
- $a=1234.345\pm 263.1$
Dadas las siguientes cifras y su error relativo, especificar de manera correcta el valor esperado (con el número correcto de cifras significativas) y su valor absoluto en el formato $a\pm \Delta a~(\varepsilon_a )$ con el error absoluto con (i) una cifra significativa y (ii) dos cifras significativas.
- $a=1.34256784,\mathrm{ }\varepsilon =12\mathrm{ }\%$
- $a=1.34256784,\mathrm{ }\varepsilon =0.1\mathrm{ }\%$
- $a=1.342567,\mathrm{ }\varepsilon =0.01\mathrm{ }\%$
- $a=0.04523,\mathrm{ }\varepsilon =20\mathrm{ }\%$
- $a=0.04523,\mathrm{ }\varepsilon =1\mathrm{ }\%$
- $a=342.7893,\mathrm{ }\varepsilon =10\mathrm{ }\%$
- $a=342.7893,\mathrm{ }\varepsilon =0.5\mathrm{ }\%$
En los ejercicios del numeral B, indicar la desviación estándar si se asume que la distribución de probabilidad es (i) normal, (ii) uniforme. Se debe que recordar que no siempre el valor absoluto en un intervalo de confianza indica la desviación estándar, pues depende del tipo de distribución de probabilidad.
D. Intervalos de confianzaPara cada uno de los ejercicios del numeral B (con los datos en la forma correcta), asumiendo el número de muestras $N$ y el nivel de confianza $p$ que se especifica, (i) indicar el error estándar y (ii) el intervalo de confianza. Se debe usar la distribución t de Student ($t_{p,n}$). Ver la tabla t-Student. Cálculo con MATLAB: tinv.
- $n=100, p=0.70$
- $n=100, p=0.95$
- $n=100, p=0.99$
- $n=100,p=0.999$
- $n=1000,p=0.70$
- $n=1000,p=0.95$
- $n=1000,p=0.99$
- $n=40,p=0.70$
- $n=40,p=0.95$
- $n=40,p=0.99$
- $n=68,p=0.96$
Dadas las siguientes magnitudes con sus intervalos de confianza y la operación que las relaciona, calcular el intervalo de confianza del resultado de la operación con 1 cifra significativa y expresar la solución en la forma $a\pm \Delta a~(\varepsilon_a)$ con (i) la fórmula de primer orden y (ii) la fórmula de segundo orden; (iii) analizar el resultado.
- $A=bh/2, b=2.34\pm 0.09, h=4.3\pm 0.4$
- $y=a^2, a=1.435\pm 0.006$
- $y=a^3,\ a=1.435\pm 0.006$
- $z=x(x+y)(x-y)^{-1}, x=1.23\pm 0.03, y=0.237\pm 0.005$
- $z=y-x, x=2.52\pm 0.01, y=2.55\pm 0.03 $
- $y=y_0+v_0t+0.5gt^2, y_0=0.000\pm 0.005, v_0=0.03234~(\varepsilon=8.3\%)$, $g=9.817845~( \varepsilon =1.4\%) , t=5.23145~(\varepsilon =5.3\%)$
- $y=\log a, a=34 \pm 2$
- $y=r\cos \theta, \theta =0.9250 \pm 0.0035, r=2.0 \pm 0.2$
- $g=\frac{4\pi l}{p^2}, l=2.34 \pm 0.01~\mathrm{m}, P=1.73 \pm 0.06~\mathrm{seg}$
A partir del código de MATLAB dado (se requiere una cuenta de MATLAB), utilizar el método de Montecarlo con $N=100,000$ para resolver los ejercicios del numeral E con un muestreo gaussiano, y analizar los resultados.
G. Método de Montecarlo con distribución uniformeA partir del código de MATLAB dado (se requiere una cuenta de MATLAB), utilizar el método de Montecarlo con $N=100,000$ para resolver los ejercicios del numeral E con un muestreo uniforme, y analizar los resultados.
H. Método “Crank Three Times”Utilizar el método “Crank Three Times” para resolver los ejercicios del numeral E con un muestreo gaussiano, y analizar los resultados. Revisar si los intervalos de confianza son simétricos.
3. Análisis de sistemas dinámicos
3.1. Curva de linealidad, puntos de equilibrio y linealización
1. Modelo SIR
3.2. Métodos de estabilidad directo e indirecto de Lyapunov
Dados los siguientes modelos no lineales, (i) aplicar el método directo de Lyapunov para determinar la estabilidad de un punto de equilibrio (si no está en (0,0) es necesario realizar un cambio de variables); (ii) aplicar el método indirecto de Lyapunov; (iii) dibujar el plano de fase con MATLAB y verificar los resultados anteriores; (iv) verificar el resultado con simulación.
- $\left\{\begin{array}{l} \dot{x}_1=x_2\\ \dot{x}_2=-x_1-\varepsilon (x_1^2-1)x_2\\ \end{array} \right.$ $ \varepsilon =0,\varepsilon <0,\varepsilon >0$
- $\left\{ \begin{array}{l} \dot{x}_1=-x_1+x_2^2\\ \dot{x}_2=-x_2\\ \end{array} \right. $
- $\left\{ \begin{array}{l} \dot{x}_1=x_1^3-4x_1-x_2\\ \dot{x}_2=x_1-x_2\\ \end{array} \right. $
- $\left\{ \begin{array}{l} \dot{x}_1=x_1(x_2-1)+u\\ \dot{x}_2=x_2(x_1-2)\\ \end{array} \right. $
- $\left\{ \begin{array}{l} \dot{x}_1=x_1(x_1^2+x_2^2-2)-4x_1x_2^2\\ \dot{x}_2 = 4x_1^2x_2+x_2(x_1^2+x_2^2-2)\\ \end{array} \right. $
- $\left\{ \begin{array}{l} \dot{x}_1=x_1(x_1^2-2x_2)(x_1^2-1)\\ \dot{x}_2=(x_1+x_2)(x_{1}^{2}-1)\\ \end{array} \right.$ $ V(\mathbf{x})=ax_1^2+bx_2^2$
- $\left\{ \begin{array}{l} \dot{x}_1=-4x_1-3x_2\\ \dot{x}_2=4x_1\\ \end{array} \right.$ $V(\mathbf{x})=\mathbf{x}^T\mathbf{Px}$
- $\left\{ \begin{array}{l} \dot{x}_1=-x_1+x_2 \\ \dot{x}_2=(x_1+x_2)senx_1-3x_2\\ \end{array} \right. $
- $\left\{ \begin{array}{l} \dot{x}_1=x_2\\ \dot{x}_2=-x_1+\varepsilon \left( \frac{x_2^3}{3}-x_2 \right)\\ \end{array} \right.$ $V(\mathbf{x})=ax_1^2+bx_2^2$
3.3. Método de estabilidad de Routh-Hurwitz
Dados los siguientes modelos o polinomios característicos, (i) aplicar las condiciones necesarias y suficientes del método de Routh-Hurwitz para determinar la estabilidad o condición de estabilidad; (ii) verificar los resultados utilizando la función routh_hurwitz de MATLAB; (iii) verificar los resultados calculando con la función roots de MATLAB las raíces características del polinomio y, para los casos de estabilidad condicional, probar con algunos valores del parámetro por dentro y fuera de la región de estabilidad.
A. Casos simplesEn el caso de sistemas inestables, determinar el número de raíces en el semiplano derecho complejo.
- $P(\lambda )=\lambda ^2+2\lambda +10$
- $P(\lambda )=\lambda ^2+2\lambda +10000$
- $P(\lambda )=\lambda ^2+2\lambda -1$
- $P(\lambda )=\lambda ^2-2\lambda -4$
- $P(\lambda )=-\lambda ^2-2\lambda -10$
- $P(\lambda )=\lambda ^3+6\lambda ^2+11\lambda +6$
- $P(\lambda )=\lambda ^3+6\lambda ^2+11\lambda -6$
- $P(\lambda )=\lambda ^3+6\lambda ^2-11\lambda +6$
- $P(\lambda )=\lambda ^3-6\lambda ^2+11\lambda +6$
- $P(\lambda )=\lambda ^4+5\lambda ^3+9\lambda ^2+7\lambda +2$
- $P(\lambda )=\lambda ^3+2\lambda ^2+2\lambda +1$
- $P(\lambda )=\lambda ^4+5\lambda ^3+6\lambda ^2+5\lambda +1$
- $P(\lambda )=\lambda ^4+5\lambda ^3+2\lambda ^2-5\lambda +1$
- $P(\lambda )=\lambda +k$
- $P(\lambda )=0.5\lambda +k$
- $P(\lambda )=\lambda ^2+(k-2)\lambda +2$
- $P(\lambda )=(\lambda +1)(\lambda +2)^2[\lambda ^2+(k-2)\lambda +2]$
- $P(\lambda )=(\lambda +1)(\lambda +2)^2[\lambda ^2+(k-2)\lambda +2]$
- $P(\lambda )=\lambda ^2+(k-2)\lambda +3-k$
- $P(\lambda )=\lambda ^2+(10-k)\lambda +k-7$
- $P(\lambda )=(k-3)\lambda ^2+(5-k)\lambda +12-3k$
- $P(\lambda )=\lambda ^3+2\lambda ^2+4\lambda +k$
- $P(\lambda )=\lambda ^3+\lambda ^2+k\lambda +3$
- $P(\lambda )=\lambda ^3+\lambda ^2+(k-5)\lambda +3$
- $P(\lambda )=\lambda ^3+\lambda ^2+(2-k)\lambda +1$
- $P(\lambda )=\lambda ^3+\lambda ^2+(2k-1)\lambda +k$
- $P(\lambda )=\lambda ^3+a\lambda ^2+b\lambda +c$
- $P(\lambda )=\lambda ^4+\lambda ^3+2\lambda ^2+\lambda +k$
- $P(\lambda )=\lambda ^4+\lambda ^3+2k\lambda ^2+\lambda +k$
- $P(\lambda )=\lambda ^4+\lambda ^3+2\lambda ^2+k\lambda +1$
- $P(\lambda )=\lambda ^4+\lambda ^3+k\lambda ^2+\lambda +1$
- $P(\lambda )=\lambda ^4+k\lambda ^3+2\lambda ^2+\lambda +1$
- $P(\lambda )=(\lambda +1)(\lambda +2)^2(\lambda ^2+K)$
- $P(\lambda )=\lambda ^3+(11+k)\lambda ^2+(10+75k)\lambda +1250k$
- $P(\lambda )=\lambda ^3+(12+k)\lambda ^2+(2+k)\lambda +25k$
- $P(\lambda )=\lambda ^3+(k-2)\lambda ^2+(2+k)\lambda +25k$
- $P(\lambda )=\lambda ^4+k\lambda ^3+2k\lambda ^2+4k\lambda +8k-16$
- $P(\lambda )=\lambda ^4+\lambda ^3+\lambda ^2+\lambda +k$
- $P(\lambda )=\lambda ^4+6\lambda ^3+11\lambda ^2+(6+k)\lambda +2k$
- $P(\lambda )=\lambda ^4+3\lambda ^3+3\lambda ^2+2\lambda +k$
- $P(\lambda )=\lambda ^4+k\lambda ^3+4\lambda ^2+7\lambda +2$
- $P(s)=s^5+s^4+10s^3+Ks^2+2Ks+K$
- $P(s)=s^4+18s^3+as^2+4s+b$
- $P(s)=s^2+(K_d+3)s+0.5K_p$
- $P(s)=s^3+k_1s^2+k_2s+k_3$
- $P(s)=s^3+100s^2+(90+10k_1k_2)s+90k_1k_2$
- $P(s)=s^3+6.8s^2+(K_d+5)s+K_p+4$
- $P(s)=s^4+21s^3+10s^2+20K_ps+60K_i$
- $s^3+as^2+(ab-1)s+2a(b-2)$
- $G(s)=\frac{s-3k}{s^4-(k-3)s^3+2s^2+k(3-k)s+k(2-k)}$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1& 0\\ 0& 0& 1\\ -1& -k& -2\\\end{matrix} \right] \mathbf{x}$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1& 0\\ 0& 0& 1\\ -k& -k& -k\\\end{matrix} \right] \mathbf{x}$
7. Sistema 7. Tip: usar la aproximación de Padé.
9. Sistema 9. Para valores de $K$ y $\tau $. Tip: usar la aproximación de Padé.
3.4. Método de estabilidad de Jury
- $P(z)=(z+0.2)(z-0.5)(z+0.7)(z-0.8)$
- $P(z)=(z+0.2)(z-0.5)(z+0.7)(z-0.8)$
- $P(z)=(z-0.5)(z-4)(z-0.25)$
- $P(z)=z^4-1.2z^3+0.07z^2+0.3z-0.08$
- $1+K\frac{0.2z+0.5}{z^2-1.2z+0.2}=0$
- $1+\frac{K(0.368z+0.264)}{z^2-1.368z+0.368}=0$
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.2& k\\ 0.3& -0.5\\\end{matrix} \right] \mathbf{x}(k)$
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.2& -0.4\\ 0.3& k\\\end{matrix} \right] \mathbf{x}(k)$
- Modelo en lazo cerrado
- Planta discreta
- Modelo en lazo cerrado
- Planta discreta
- Modelo en lazo cerrado
- Planta continua para discretizar con un retenedor de orden cero
- Modelo en lazo cerrado
- Planta continua para discretizar con un retenedor de orden cero
3.5. Método de estabilidad del lugar de las raíces con MATLAB
- $G(s)=\frac{1800}{s(s+4)(s+40)}$
- $G(s)=\frac{(s+25)(s+50)}{s(s+1)(s+10)}$
- $G(s)=\frac{1}{s^2+2s-3}$
- $G(s)=\frac{s+6}{s(s+4)(s+5)(s+7)}$
- $G(s)=\frac{s+1}{s^2(s+6)}$
- $G(s)=\frac{1}{s(s^2+2s+4)}$
- $G(s)=\frac{s+2}{(s^2+2s+2)(s^2+4s+5)}$
- $G(s)=\frac{(s+2)(s+8)}{s^3}$
- $G(s)=\frac{s+1}{s(s-2)(s+3)}$
- $P(\lambda )=(\lambda +1)(\lambda +2)^2(\lambda ^2+K)$
- $P(\lambda )=(\lambda +1)(\lambda +2)^2(\lambda ^2+K\lambda +2)$
- $P(\lambda )=\lambda ^2+(k-1)\lambda +(3-k)$
- $P(\lambda )=\lambda ^3+(11+k)\lambda ^2+(10+75k)\lambda +1250k$
- $P(\lambda )=\lambda ^3+(12+k)\lambda ^2+(2+k)\lambda +25k$
- $P(\lambda )=\lambda ^3+(k-2)\lambda ^2+(2+k)\lambda +25k$
- $P(\lambda )=\lambda ^4+k\lambda ^3+2k\lambda ^2+4k\lambda +8k-16$
- $P(\lambda )=\lambda ^4+\lambda ^3+\lambda ^2+\lambda +k$
- $P(\lambda )=\lambda ^3+2\lambda ^2+4\lambda +k$
- $P(\lambda )=\lambda ^4+6\lambda ^3+11\lambda ^2+(6+k)\lambda +2k$
- $P(\lambda )=\lambda ^4+3\lambda ^3+3\lambda ^2+2\lambda +k$
- $P(\lambda )=\lambda ^4+k\lambda ^3+4\lambda ^2+7\lambda +2$
- $P(s)=s^5+s^4+10s^3+Ks^2+2Ks+K$
- $P(s)=s^4+18s^3+as^2+4s+b$
- $P(s)=s^2+(K_d+3)s+0.5K_p$
- $P(s)=s^3+k_1s^2+k_2s+k_3$
- $P(s)=s^3+100s^2+(90+10k_1k_2)s+90k_1k_2$
- $P(s)=s^3+6.8s^2+(K_d+5)s+K_p+4$
- $P(s)=s^4+21s^3+10s^2+20K_ps+60K_i$
- $P(s)=s^3+as^2+(ab-1)s+2a(b-2)$
- $G(s)=\frac{s-3k}{s^4-(k-3)s^3+2s^2+k(3-k)s+k(2-k)}$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1& 0\\ 0& 0& 1\\ -1& -k& -2\\\end{matrix} \right] \mathbf{x}$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1& 0\\ 0& 0& 1\\ -k& -k& -k\\\end{matrix} \right] \mathbf{x}$
1. Diagrama de bloques 1:
D. Caso de tiempo discreto
- $P(z)=(z+0.2)(z-0.5)(z+0.7)(z-0.8)$
- $P(z)=(z-1)(z+0.5)(z-0.8)$
- $P(z)=(z-0.5)(z-4)(z-0.25)$
- $P(z)=z^4-1.2z^3+0.07z^2+0.3z-0.08$
- $1+K\frac{0.2z+0.5}{z^2-1.2z+0.2}=0$
- $1+\frac{K(0.368z+0.264)}{z^2-1.368z+0.368}=0$
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.2& k\\ 0.3& -0.5\\\end{matrix} \right] \mathbf{x}(k)$
- $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.2& -0.4\\ 0.3& k\\\end{matrix} \right] \mathbf{x}(k)$
- Lazo cerrado:
- Diagrama de bloques:
3.6. Características de la respuesta temporal
Dados los siguientes modelos, (i) para modelos de orden 1 y 2 determinar las características temporales (tiempo de crecimiento, tiempo de pico, sobreimpulso máximo, tiempo de establecimiento y valor final) matemáticamente (consultar del libro las respectivas fórmulas) y a partir del gráfico de la respuesta temporal; (ii) para modelos de orden mayor que 2 obtener las características temporales a partir del gráfico de la respuesta temporal y matemáticamente utilizando la aproximación a un modelo de orden 1 o 2 (reducción del orden), para el caso sin y con oscilaciones, respectivamente; (iii) verificar los resultados anteriores con las funciones stepplot y stepinfo de MATLAB.
- $G(s)=\frac{0.4}{s+2}$
- $G(s)=\frac{1}{s+0.2}$
- $G(s)=\frac{e^{-2s}}{s+1}$
- $G(s)=\frac{3}{s^2+2s+4}$
- $G(s)=\frac{3}{s^2+2s+0.6}$
- $G(s)=\frac{4e^{-3s}}{s^2+2s+6}$
- $G(s)=\frac{4e^{-2s}}{(s+2)(s+0.2)}$
- $G(s)=\frac{3}{(s+2)(s^2+2s+4)}$
- $G(s)=\frac{6e^{-4s}}{(s+10)(s^2+2s+4)}$
- $G(s)=\frac{3}{(s+1)(s+5)(s+6)^2}$
- $G(s)=\frac{3}{(s+1)^2(s+2)^3}$
- $G(s)=\frac{10}{(s+2)(s^2+2s+4)}$
- $G(s)=\frac{10}{(s+6)(s^2+2s+4)}$
- $G(s)=\frac{10(s+3)}{(s+3.2)(s+6)(s^2+2s+4)}$
- $G(s)=\frac{60}{(s^2+2s+2)(s^2+12s+34)}$
- $G(s)=\frac{30(s+1)}{(s+2)(s+3)(s+4)}$
- $G(s)=\frac{60(s+2.2)}{(s+2)(s+3)(s+4)}$
- $G(s)=\frac{60(s+0.8)}{(s+1)(s+2)(s+10)}$
3.7. Diagrama de Bode con MATLAB
Obtener el diagrama de Bode con MATLAB de modelos de tiempo continuo y tiempo discreto y analizar los resultados.
Dados los siguientes modelos de tiempo continuo y discreto, (i) obtener el diagrama de Bode de los siguientes sistemas utilizando la función bode de MATLAB; (ii) especificar la frecuencia de resonancia, pico de resonancia, ancho de banda y zonas en las cuales el sistema funciona como un amplificador o atenuador; (iii) calcular la razón de corte y cambio de fase, y explicar porque el sistema es o no de fase mínima; (iv) obtener del diagrama de Bode la respuesta temporal cuando la entrada es $u=2\sin 3t$ y $u=10\sin 20t$, y verificar el resultado a partir de la respuesta temporal usando la función lsim de MATLAB; (v) determinar a partir del diagrama de Bode el margen de ganancia y el margen de fase para la estabilidad en lazo cerrado, y verificar el resultado con la función lsim de MATLAB, con valores de la ganancia $K$ y el retardo $\tau$ dentro y fuera de los intervalos de estabilidad calculados; (vi) diseñar un programa de MATLAB que calcule el diagrama de Bode a partir del módulo y fase de números complejos, y comparar los resultados con los de la función bode de MATLAB.
- $G(s)=\frac{1}{s+1}$
- $G(s)=\frac{e^{-2s}}{s+1}$
- $G(s)=\frac{1}{s-1}$
- $G(s)=\frac{1}{(s+1)^2}$
- $G(s)=\frac{s-1}{(s+1)^2}$
- $G(s)=\frac{e^{-0.5s}}{(s+1)^2}$
- $G(s)=\frac{1}{s^2+2s+10}$
- $G(s)=\frac{10}{s^2+2s+10}$
- $G(s)=\frac{s+1}{s^2+2s+10}$
- $G(s)=\frac{s-1}{s^2+2s+10}$
- $G(s)=\frac{1}{s(s^2+2s+10)}$
- $G(s)=\frac{1}{s^2(s^2+2s+10)}$
- $G(s)=\frac{e^{-2s}}{s^2+2s+10}$
- $G(s)=\frac{1}{s^2+2s-3}$
- $G(s)=\frac{s+10}{s^2+1001s+1000}$
- $G(s)=\frac{1}{(s+1)(s+10)(s^2+2s+10)}$
- $G(s)=\frac{s+2}{(s-1)(s+10)(s^2+2s+10)}$
- $G(s)=\frac{s^2+0.1s+7.5}{s^2(s^2+0.12s+9)}$
- $G(s)=\frac{200s(0.05s+1)(3s+1)}{(10s+1)(0.02s+1)(5.4s+1)}$
- $G(s)=\frac{10^5s(s+100)}{(s+10)^2(s^2+400s+10^6)}$
- $G(s)=\frac{s^2+18s+100}{s^2+6.06s+102.01}$
- $G(s)=\frac{1.25}{(s+1)(s^2+0.5s+1)}$
- $G(s)=\frac{1.25e^{-1.5s}}{(s+1)(s^2+0.5s+1)}$
- $G(s)=\frac{1.25(s-2)}{(s+1)(s^2+0.5s+1)}$
- $G(s)=\frac{40}{s(s+1)(s+8)(s+10)}$
- $G(s)=\frac{1800}{s(s+4)(s+40)}$
- $G(s)=\frac{(s+25)(s+50)}{s(s+1)(s+10)}$
Discretizar con la función c2d de MATLAB cada modelo anterior con un período de muestreo de 0.1 seg y (i) obtener el diagrama de Bode con la función bode de MATLAB y compararlo con el del modelo continuo; (ii) obtener los márgenes de estabilidad a partir del modelo discreto y compararlos con los del modelo continuo (¿aumentan o disminuyen?).
3.8. Selección del período de muestreo y sus efectos
- $G(s)=\frac{2}{s+4}$
- $G(s)=\frac{2}{s+0.25}$
- $G(s)=\frac{1}{s^2+2s+0.2}$
- $G(s)=\frac{1}{s^2+2s+4}$
- $G(s)=\frac{e^{-2s}}{s^3+2s^2+3s+4}$
- $G(s)=\frac{1}{s-1}$
- $G(s)=\frac{1}{s^2+2s-4}$
4. Diseño de sistemas básicos de control lineal
4.1. Eliminación del error en estado estacionario
Dados los siguientes modelos, (i) definir el tipo de sistema (según el número de integradores); (ii) determinar a partir de la tabla dada en el libro el error en estado estacionario en lazo cerrado ante una entrada escalón (posición), rampa (velocidad) y parábola (aceleración); (iii) verificar si el sistema en lazo cerrado es estable y, si no lo es, aplicar el método de estabilidad de Routh-Hurwitz para hallar un controlador $G_c(s)=k$ (Proporcional continuo), $G_c(z)=k$ (Proporcional discreto), $G_c(s)=k_1+k_2/s$ (Proporcional-Integral continuo) o $G_c(z)=(k_1z+k_2)/(z-1)$ (Proporcional-Integral discreto) que estabilice el sistema; (iv) simular en un Script de Matlab o con Simulink para verificar el resultado anterior.
A. Caso de tiempo continuo- $G(s)=\frac{2}{s+3}$
- $G(s)=\frac{2}{s(s+3)}$
- $G(s)=\frac{2}{s^2(s+3)}$
- $G(z)=\frac{1}{z-0.5}$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -2& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 0\\ 0\\\end{array} \right] u,y=\left[ \begin{matrix} 0& 0& 1\\\end{matrix} \right] \mathbf{x}$
- $G(z)=\frac{1}{z(z-0.5)}$
- $G(z)=\frac{1}{(z-0.5)(z-1)}$
- $G(z)=\frac{1}{(z-0.5)(z-1)^2}$
- $G(z)=\frac{z}{z^4-1}$
4.2. Control de asignación de polos y ceros con enfoque polinomial
Dados los siguientes modelos, (i) obtener la función de transferencia deseada de tiempo continuo si el requerimiento de diseño exige que la respuesta temporal en lazo cerrado tenga las siguientes características: $t_p \simeq 0.5~\mathrm{seg}$, $e_{ss}=0$, $M_p=10~\%$; (ii) obtener el período de muestreo a partir del tiempo de crecimiento y discretizar la función de transferencia de la planta continua (si el modelo es inestable se debe utilizar la función de transferencia deseada en lazo cerrado); (iii) diseñar un controlador de asignación de polos y ceros de tiempo discreto que cumpla con las características anteriores; (iv) simular con MATLAB o Simulink y verificar el correcto comportamiento del sistema de control, incluyendo una perturbación tipo escalón y cambios en la señal de referencia; (v) realizar un análisis de sensibilidad e incertidumbre con diferentes incertidumbres de los parámetros de la planta continua; (vi) dar el pseudocódigo del controlador; (vii) analizar los resultados, prestando atención al esfuerzo de control. Ver los casos de estudio como referencia de la tarea a realizar.
- $G(s)=\frac{2}{s+3}$
- $G(s)=\frac{1}{s-2}$
- $G(s)=\frac{1}{(s+1)(s+2)}$
- $G(s)=\frac{1}{s^2}$ (integrador doble)
- $G(s)=\frac{2}{(s+0.5)(s+5)}$
- $G(s)=\frac{2}{(s+0.5)(s+5)(s+6)}$
- $G(s)=\frac{1}{s^2+2s+2}$
- $G(s)=\frac{2e^{-2s}}{s+3}$
- $G(s)=\frac{e^{-0.5s}}{s-1}$
- $G(s)=\frac{4}{s^2+0.8}$
- $G(s)=\frac{1}{(s-1)(s-2)}$
- $G(s)=\frac{s+1}{(s+1.2)(s+3)}$
4.3. Controlador PID - Diseño y simulación
Dados los modelos de los ejercicios propuestos 4.2, diseñar controladores P, PI y PID de tiempo discreto teniendo en cuenta las siguientes tareas: (i) diseño por el método de Ziegler-Nichols de la curva de reacción (cuando aplique); (ii) diseño por el método de Ziegler-Nichols de sensibilidad; (iii) diseño por el método de Chien-Hrones-Reswick; (iv) diseño con la herramienta pidTuner de MATLAB; (v) diseño por asignación de polos del PID (el modelo deseado depende de las características deseadas); (vi) simulación de cada sistema de control con un cambio de la referencia, con una perturbación tipo escalón y con una saturación arbitraria y adecuada del actuador (implementar un método antisaturación); (vii) especificación del pseudocódigo del controlador; (viii) interpretación de los resultados, prestando atención a la regulabilidad y a la acción de control. Ver los casos de estudio como referencia de la tarea a realizar.
4.4. Predictor de Smith en control - Diseño y simulación
Dados los siguientes modelos de plantas continuas con retardo, implementar un predictor de Smith y realizar las siguientes tareas: (i) diseño de un controlador PID de tiempo discreto (por ajuste heurístico o por asignación de polos); (ii) diseño del controlador discreto sin el predictor de Smith; (iii) simulación de cada sistema de control con un cambio de la referencia; (iv) análisis de incertidumbre; (v) interpretación de los resultados.
- $G(s)=\frac{2e^{-2s}}{s+3}$
- $G(s)=\frac{e^{-0.5s}}{s-1}$
- $G(s)=\frac{4e^{-3s}}{(s+1)(s-2)}$
4.5. Controlador de asignación de polos por realimentación del estado
Dados los siguientes modelos de plantas de tiempo continuo, (i) determinar la controlabilidad del modelo lineal, incluyendo el número de condición; (ii) determinar el período de muestreo, de acuerdo con el tiempo de crecimiento de la respuesta temporal a un escalón, y discretizar el modelo de la planta; (iii) diseñar con la función place de MATLAB un controlador de asignación de polos por realimentación del estado de tiempo discreto de manera que el sistema se estabilice de manera más rápida en el punto de equilibrio (probar con diferentes ubicaciones de los polos deseados y verificar los polos en lazo cerrado); (iv) diseñar con MATLAB un controlador con integrador y eliminación del error en estado estacionario para una entrada escalón, una salida y diferentes ubicaciones de los polos discretos deseados (en el origen, cerca de 0.5 y cerca de 0.9); (v) simular con MATLAB o Simulink cada sistema de control con un cambio de la referencia (cuando aplique), una perturbación tipo escalón en un momento determinado y una saturación arbitraria y adecuada del actuador; (vi) interpretar los resultados, prestando atención al esfuerzo de control y a la saturación. Ver los casos de estudio como referencia de la tarea a realizar.
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 0\\ -3& 3\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 3\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -1& 0\\ 0& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -1& 0\\ 0& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 1& 0\\ 2& -3\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -1& 0\\ 0& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{matrix} 1& 0\\ 0& -2\\\end{matrix} \right] \mathbf{u}$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -0.2& 0\\ 0.25& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 2\\ 0\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 1& 1\\ 1& 2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 2\\ 0\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 2\\ 2& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0.5\\ 0\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -10& -0.5\\ 0.5& -1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 10\\ 0\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -5& -2& -1\\ 4& 0& 0\\ 0& 1& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0.5\\ 0\\ 0\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -5& -4& 0\\ 1& 0& 0\\ 0& 1& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 2\\ 0\\ 0\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -3& -3& -2\\ 2& 0& 0\\ 0& 1& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0.5\\ 0\\ 0\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -2.6& -2.6& -1.2\\ 2& 0& 0\\ 0& 1& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 0\\ 0\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -1& 0& 0\\ 0& 1& 0\\ 0& 1& -2\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ -1\\ 0\\\end{array} \right] u$ (sistema estabilizable)
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -3& -3& -2\\ 2& 0& 0\\ 0& 1& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{matrix} 0.5& 0\\ 0& 1\\ 0& 0\\\end{matrix} \right] \mathbf{u}$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} -1& 1& 0\\ 1& -3& 1\\ 0& 1& -1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{matrix} 0& 0\\ 1& 2\\ 0& 2\\\end{matrix} \right] \mathbf{u}$
- $\left[ \begin{array}{c} \dot{x}_1\\ \dot{x}_2\\ \dot{x}_3\\ \dot{x}_4\\\end{array} \right] =\left[ \begin{matrix} 0& 0& 1& 0\\ 0& 0& 0& 1\\ -\frac{k_a+k_c}{m_a}& \frac{k_c}{m_a}& -\frac{f_a}{m_a}& 0\\ \frac{k_c}{m_b}& -\frac{k_b+k_c}{m_b}& 0& -\frac{f_b}{m_b}\\\end{matrix} \right] \left[ \begin{array}{c} x_1\\ x_2\\ x_3\\ x_4\\\end{array} \right] +\left[ \begin{array}{c} 0\\ 0\\ \frac{1}{m_a}\\ 0\\\end{array} \right] u$ $m_a=m_b=1,f_a=f_b=0.7,k_a=k_b=k_c=5$
- $\left[ \begin{array}{c} \dot{x}_1\\ \dot{x}_2\\\end{array} \right] =\left[ \begin{matrix} 0& 1/C\\ -1/L& -R/L\\\end{matrix} \right] \left[ \begin{array}{c} x_1\\ x_2\\\end{array} \right] +\left[ \begin{array}{c} 0\\ 1/L\\\end{array} \right] u$, $R = 100, L = 0.1, C=0.001$
5. Identificación de sistemas dinámicos
5.1. Procedimiento de identificación de sistemas
Para los siguientes procesos, (i) especificar las entradas, salidas, posibles perturbaciones y parámetros físicos del sistema; (ii) explicar cada etapa del proceso de identificación con información específica del modelo (consultar en internet por un posible modelo matemático o hacer suposiciones del orden y retardo); (iii) si el modelo es no lineal, explicar cómo se deben tomar los datos para la obtención de un modelo lineal; (v) indicar y explicar si el sistema se debe o puede modelar como una serie de tiempo. Tomar como referencia el ejercicio resuelto 5.13.
- Tanque de almacenamiento de agua
- Ducha de gas con agua caliente
- Olla a presión con agua sobre una estufa de gas
- Aula de clase con aire acondicionado
- El habla
- Circuito eléctrico
- Sistema masa-resorte
- Inflación de un país
- Sistema de control adaptativo de crucero (ACC)
- Péndulo simple
- Sistema ecológico con presas y depredadores
- La tasa representativa del mercado
- Aprendizaje profesor-alumno
- Formación de los hijos en una familia
- Epidemia en una ciudad
- Páncreas artificial
- Varilla en posición vertical sobre la mano de una persona
- Lavado de ropa en una lavadora automática
5.2. Métodos no paramétricos de identificación de la respuesta temporal
Dadas las siguientes funciones de transferencia y utilizando MATLAB, (i) obtener la respuesta temporal "experimental" a una entrada escalón unitario con la función step, adicionando un pequeño ruido a la salida con la función randn; (ii) a partir de los "datos experimentales" anteriores calcular la función de transferencia experimental por el método no paramétrico de la respuesta temporal de primer orden (si la respuesta no tiene oscilaciones) o segundo orden subamortiguado (si la respuesta tiene oscilaciones); (iii) validar con el escalón el modelo experimental indicando el porcentaje de ajuste y el análisis residual con la función whiteness_test.
- $G(s)=\frac{2}{s+4}$ (si el modelo corresponde a un circuito eléctrico RL, estimar los parámetros)
- $G(s)=\frac{4e^{-2.2s}}{s+0.5}$
- $G(s)=\frac{5(s+3.9)e^{-s}}{(s+4)(s+10)(s^2+s+2)}$
- $G(s)=\frac{2}{s^2+2s+2}$
- $G(s)=\frac{2e^{-s}}{3s+2}$
- $G(s)=\frac{4e^{-2s}}{s^2+s+1}$
- $G(s)=\frac{2}{(s+0.5)(s+5)}$
- $G(s)=\frac{(s+1.1)e^{-3.1s}}{(s+0.1)(s+1)(s+3)}$
- $G(s)=\frac{3e^{-s}}{(s+5)(s^2+s+2)}$
- $G(s)=\frac{2}{(s+1)(s+2)}$
- $G(s)=\frac{3e^{-s}}{s^2+3s+5}$
- $G(s)=\frac{5(s+2.1)e^{-s}}{(s+2)(s^2+s+2)}$
- $G(s)=\frac{2e^{-2s}}{(s+1)^2(s^2+2s+6)}$
5.3. Método de correlación de identificación no paramétrica
5.4. Método espectral de identificación no paramétrica
5.5. Estructuras del modelo lineal discreto en identificación lineal
Para los órdenes (na, nb), retardo (nk) y número de entradas y salidas (m, p) del modelo discreto de la planta que se dan a continuación (considerando los polinomios de la perturbación del mismo orden del proceso cuando sea necesario), (i) especificar las estructuras ARX, ARMAX, OE, FIR, BJ y ARARX en forma de operadores de desplazamiento hacia atrás; (ii) dar la función de transferencia discreta de la planta; (iii) obtener la forma regresiva para la estructura ARX utilizando los residuos $e(t)$, mientras que para los otras estructuras utilizar $\varepsilon(t)$.
- m = 1, p = 1, na = 2, nb = 2, nk = 2
- m = 1, p = 1, na = 1, nb = 3, nk = 4
- m = 1, p = 1, na = 2, nb = 2, nk = 1
- m = 1, p = 1, na = 3, nb = 6, nk = 3
- m = 1, p = 1, na = 2, nb = 4, nk = 3
- m = 1, p = 1, na = 5, nb = 8, nk = 2
- m = 1, p = 1, na = 2, nb = 5, nk = 4
- m = 1, p = 1, na = 1, nb = 3, nk = 0
- m = 2, p = 1, na = 1, nb = 1, nk = 1
- m = 1, p = 2, na = 1, nb = 1, nk = 1
- m = 2, p = 2, na = 1, nb = 1, nk = 1
- m = 2, p = 3, na = 2, nb = 4, nk = 3
- m = 3, p = 2, na = 2, nb = 4, nk = 3
5.6. Método de identificación de mínimos cuadrados
Para los siguientes modelos y con la implementación en MATLAB, (i) indicar los pasos para la identificación (planificación experimental); (ii) obtener los datos experimentales sintéticos con un período de muestreo adecuado, uso de una entrada PRBS con la función idinput y la adición a la salida de un pequeño ruido tipo ARX, $v=[1/A(q^{-1}]e(t)$, generando $e(t)$ con la función randn ; (iii) implementar el método de mínimos cuadrados y el cálculo de los intervalos de confianza por la fórmula del método y el método de bootstrapping para el mejor modelo; (iv) validar el modelo comparando la salida experimental con la estimada con una entrada escalón y una señal sinusoidal, y calcular el porcentaje de ajuste; (v) realizar el análisis residual con la función whiteness_test; (vi) obtener el mapa de polos y ceros con la función pzmap para detectar una posible reducción del orden; (vii) documentar el modelo final con los respectivos intervalos de confianza; (viii) verificar los resultados con la función arx; (ix) interpretar los resultados.
- $G(s)=\frac{2}{s+4}$
- $G(s)=\frac{4e^{-2.2s}}{s+0.5}$
- $G(s)=\frac{2}{s^2+2s+2}$
- $G(s)=\frac{4e^{-2s}}{s^2+s+1}$
- $G(s)=\frac{3e^{-s}}{(s+5)(s^2+s+2)}$
- $G(s)=\frac{5(s+3.9)e^{-s}}{(s+4)(s+10)(s^2+s+2)}$
5.7. Método de identificación de la variable instrumental
5.8. Método de identificación del error de predicción
5.9. Métodos recursivos de identificación de sistemas
5.10. Identificación de sistemas con datos reales
Dados los siguientes datos experimentales de procesos reales SISO que se encuentran en Internet en la base de datos Daisy, (i) importar los datos a MATLAB (los datos en los archivos *.dat pueden abrirse e importarse en MATLAB como una tabla o matriz numérica); (ii) leer la descripción para tener un conocimiento previo del sistema e identificar el período de muestreo y las entradas y salidas (complementar la descripción del proceso a partir de información en bases de datos bibliográficas e Internet); (iii) graficar la entrada y la salida para tener idea de la forma de los datos experimentales; (iv) utilizar la interfaz gráfica del System Identification Toolbox de MATLAB para obtener el mejor modelo; (v) documentar el mejor modelo; (vi) interpretar los resultados.
- 97-002
- 96-004
- 96-006
- 96-007
- 96-008
- 96-009
- 99-001
6. Estimación del estado
6.1. Observadores de estado lineal para sistemas dinámicos
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 0& 1\\ 3& 0\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 0\\ 0& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 0\\ -3& 3\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 1\\ 3\\\end{array} \right] u$
- $\dot{\mathbf{x}}=\left[ \begin{matrix} 2& 0\\ 0.02& 1\\\end{matrix} \right] \mathbf{x}+\left[ \begin{array}{c} 0\\ 1\\\end{array} \right] u$
- $\left\{ \begin{array}{l} \dot{x}_1=x_2 \\ \dot{x}_2=-x_1+0.1(1-x_{1}^{2})x_2\\\end{array} \right. $
- $\left\{ \begin{array}{l} \dot{x}_1=ax_1x_2+u \\ \dot{x}_2=x_{1}^{2}-bx_1x_2\\\end{array} \right. $
- $\left\{ \begin{array}{l} \dot{x}_1=x_2\\ \dot{x}_2=-\frac{g}{l}\sin x_1-\frac{f}{m}x_2+\frac{u}{ml}\\\end{array} \right. $
- $\left\{ \begin{array}{l} \dot{x}_1=\alpha x_1-\beta x_1x_2+u\\ \dot{x}_2=\delta x_1x_2-\gamma x_2\\\end{array} \right. $
- $\left\{ \begin{array}{l} \dot{x}_1=-\frac{k_1}{A}\sqrt{x_1-x_2}+\frac{a}{A}u\\ \dot{x}_2=-\frac{k_2}{A}\sqrt{x_2}+\frac{k_1}{A}\sqrt{x_1-x_2}-\frac{k_2}{A}u\sqrt{x_2}\\\end{array} \right. $
- $\left\{ \begin{array}{l} \dot{x}_1=x_2\\ \dot{x}_2=9.8-\frac{2x_{3}^{2}}{x_1}-0.1x_2\\ \dot{x}_3=0.01x_2-10x_3+10u\\\end{array} \right. $
.jpg)


























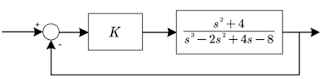
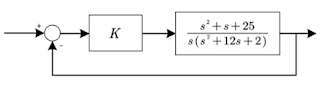


Comentarios