EP3.5. Método de estabilidad del lugar de las raíces con MATLAB

Dados los siguientes modelos matemáticas, (i) obtener por el método del lugar de las raíces (función rlocus de MATLAB) el intervalo de valores de $K$ que estabiliza el sistema (si el modelo tiene retardo utilizar la aproximación de Padé); (ii) marcar en el diagrama del lugar de la raíces los siguientes elementos: polos y ceros en lazo abierto, puntos de ruptura, puntos y valores de estabilidad crítica; (iii) verificar el resultado por el método de Routh-Hurwitz; (iv) verificar los resultados calculando con la función roots de MATLAB las raíces características con algunos valores de $K$ por dentro y fuera de la región de estabilidad.

A. Estabilidad en lazo cerrado a partir de la función de transferencia en lazo abierto

1. $G(s)=\frac{1800}{s(s+4)(s+40)}$
2. $G(s)=\frac{(s+25)(s+50)}{s(s+1)(s+10)}$
3. $G(s)=\frac{1}{s^2+2s-3}$
4. $G(s)=\frac{s+6}{s(s+4)(s+5)(s+7)}$
5. $G(s)=\frac{s+1}{s^2(s+6)}$
6. $G(s)=\frac{1}{s(s^2+2s+4)}$
7. $G(s)=\frac{s+2}{(s^2+2s+2)(s^2+4s+5)}$
8. $G(s)=\frac{(s+2)(s+8)}{s^3}$
9. $G(s)=\frac{s+1}{s(s-2)(s+3)}$

B. Estabilidad a partir de la ecuación característica

1. $P(\lambda )=(\lambda +1)(\lambda +2)^2(\lambda ^2+K)$
2. $P(\lambda )=(\lambda +1)(\lambda +2)^2(\lambda ^2+K\lambda +2)$
3. $P(\lambda )=\lambda ^2+(k-1)\lambda +(3-k)$
4. $P(\lambda )=\lambda ^3+(11+k)\lambda ^2+(10+75k)\lambda +1250k$
5. $P(\lambda )=\lambda ^3+(12+k)\lambda ^2+(2+k)\lambda +25k$
6. $P(\lambda )=\lambda ^3+(k-2)\lambda ^2+(2+k)\lambda +25k$
7. $P(\lambda )=\lambda ^4+k\lambda ^3+2k\lambda ^2+4k\lambda +8k-16$
8. $P(\lambda )=\lambda ^4+\lambda ^3+\lambda ^2+\lambda +k$
9. $P(\lambda )=\lambda ^3+2\lambda ^2+4\lambda +k$
10. $P(\lambda )=\lambda ^4+6\lambda ^3+11\lambda ^2+(6+k)\lambda +2k$
11. $P(\lambda )=\lambda ^4+3\lambda ^3+3\lambda ^2+2\lambda +k$
12. $P(\lambda )=\lambda ^4+k\lambda ^3+4\lambda ^2+7\lambda +2$
13. $P(s)=s^5+s^4+10s^3+Ks^2+2Ks+K$
14. $P(s)=s^4+18s^3+as^2+4s+b$
15. $P(s)=s^2+(K_d+3)s+0.5K_p$
16. $P(s)=s^3+k_1s^2+k_2s+k_3$
17. $P(s)=s^3+100s^2+(90+10k_1k_2)s+90k_1k_2$
18. $P(s)=s^3+6.8s^2+(K_d+5)s+K_p+4$
19. $P(s)=s^4+21s^3+10s^2+20K_ps+60K_i$
20. $P(s)=s^3+as^2+(ab-1)s+2a(b-2)$
21. $G(s)=\frac{s-3k}{s^4-(k-3)s^3+2s^2+k(3-k)s+k(2-k)}$
22. $\dot{\mathbf{x}}=\left[ \begin{matrix} 0&  1&  0\\ 0&  0&  1\\ -1&  -k&  -2\\\end{matrix} \right] \mathbf{x}$
23. $\dot{\mathbf{x}}=\left[ \begin{matrix} 0&  1&  0\\ 0&  0&  1\\ -k&  -k&  -k\\\end{matrix} \right] \mathbf{x}$

C. Estabilidad en lazo cerrado

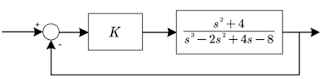
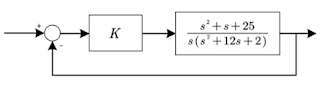
 1. Diagrama de bloques:

2. Diagrama de bloques:

3. Diagrama de bloques:

4. Diagrama de bloques:

5. Diagrama de bloques:

6. Diagrama de bloques:

7. Diagrama de bloques:

8. Diagrama de bloques:

D. Caso de tiempo discreto

1. $P(z)=(z+0.2)(z-0.5)(z+0.7)(z-0.8)$
2. $P(z)=(z-1)(z+0.5)(z-0.8)$
3. $P(z)=(z-0.5)(z-4)(z-0.25)$
4. $P(z)=z^4-1.2z^3+0.07z^2+0.3z-0.08$
5. $1+K\frac{0.2z+0.5}{z^2-1.2z+0.2}=0$
6. $1+\frac{K(0.368z+0.264)}{z^2-1.368z+0.368}=0$
7. $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.2&  k\\ 0.3&  -0.5\\\end{matrix} \right] \mathbf{x}(k)$
8. $\mathbf{x}(k+1)=\left[ \begin{matrix} 0.2&  -0.4\\ 0.3&  k\\\end{matrix} \right] \mathbf{x}(k)$
9. Lazo cerrado:
• Diagrama de bloques: